
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Тренировочное задание
|
|
1. В таблице представлен временной ряд некоторого показателя. На основе показателей ряда необходимо получить точечные и интервальные прогнозы на двухлетний период упреждения.
Таблица 6.1 - Информация периода наблюдения
| Годы | 1985 | 1986 | 1987 | 1988 | 1989 | 1990 | 1991 | 1992 | 1993 | 1994 |
| Уфакт | 27, 8 | 27, 5 | 27, 4 | 27, 5 | 27, 4 | 27, 4 | 24, 6 | 23, 9 | 23, 7 | 23, 5 |
| Годы | 1995 | 1996 | 1997 | 1998 | 1999 | 2000 | 2001 | 2002 | 2003 | 2004 |
| Уфакт | 22, 3 | 21, 6 | 21, 2 | 20, 0 | 20, 0 | 19, 7 | 18, 5 | 18, 1 | 16, 9 | 16, 7 |
По данным таблицы построим графики значений и добавим линии тренда с помощью диаграммы Excel в виде линейной, логарифмической, степенной, экспоненциальной и полиномиальной функций. Полученные результаты объединим в таблицу для выбора наиболее предпочтительной модели.
Таблица 6.2 - Аппроксимирующие функции
| Модель тренда | 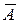
| 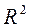
| σ | |
| линейная | y = -0, 6407*t + 29, 512 | 1, 913 | 0, 969 | 0, 668 |
| логарифмическая | y = -4, 0173*ln(t) + 31, 423 | 5, 781 | 0, 784 | 1, 752 |
| степенная | y = 32, 741*t-0, 1743. | 6, 490 | 0, 755 | 2, 032 |
| экспоненциальная | y = 30, 284*e-0, 0283*t | 2, 267 | 0, 965 | 0, 792 |
| полиномиальная | y = -0, 0073*t2 – 0, 4947*t + 29, 001 | 1, 905 | 0, 972 | 0, 635 |
По показателям адекватности (средняя ошибка аппроксимации, коэффициент детерминации и стандартное отклонение) для прогнозирования выбираем полиномиальную функцию. Используя эту модель, можно рассчитать точечные и интервальные прогнозы. Точечные прогнозы:
y21 = -0.0073*212 – 0.4947*21 + 29.001 = 15.393
y22 = -0.0073*222 – 0.4947*22 + 29.001 = 16.584
Расчет величин интервалов:
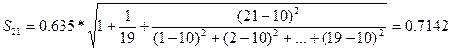
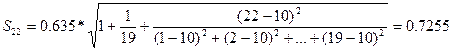
Интервальные прогнозы:
y21 = 15, 393 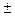 0, 7142;
0, 7142;
y22 = 14, 584 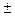 0, 7255.
0, 7255.
2. Проверим гипотезу о наличии автокорреляции в остатках с помощью критерия Дарбина-Уотсона для аддитивной модели временного ряда. Исходные данные и промежуточные расчеты заносим в таблицу (6.3).
Фактическое значение критерия Дарбина-Уотсона для данной модели составляет:
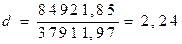 .
.
Сформулируем гипотезы: Н0 – в остатках нет автокорреляции; Н1 – в остатках есть положительная автокорреляция; 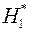 – в остатках есть отрицательная автокорреляция. Зададим уровень значимости
– в остатках есть отрицательная автокорреляция. Зададим уровень значимости 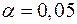 . По таблице значений критерия Дарбина-Уотсона определим для числа наблюдений
. По таблице значений критерия Дарбина-Уотсона определим для числа наблюдений 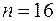 и числа независимых параметров модели
и числа независимых параметров модели 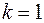 (мы рассматриваем только зависимость от времени
(мы рассматриваем только зависимость от времени 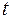 ) критические значения
) критические значения 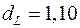 и
и 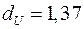 . Фактическое значение
. Фактическое значение 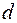 -критерия Дарбина-Уотсона попадает в интервал
-критерия Дарбина-Уотсона попадает в интервал 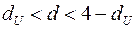 (1, 37< 2, 24< 2, 63). Следовательно, гипотеза
(1, 37< 2, 24< 2, 63). Следовательно, гипотеза 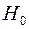 об отсутствии автокорреляции в остатках подтверждается.
об отсутствии автокорреляции в остатках подтверждается.
Таблица 6.3 - Исходные данные 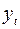 и промежуточные расчета
и промежуточные расчета
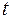
| 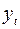
| ε t | 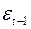
| 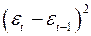
| 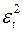
|
| -5, 252 | – | – | 27, 584 | ||
| -35, 843 | -5, 252 | 935, 8093 | 1284, 7 | ||
| -74, 183 | -35, 843 | 1469, 956 | 5503, 1 | ||
| 48, 937 | -74, 183 | 15158, 53 | 2394, 8 | ||
| -26, 946 | 48, 937 | 5758, 23 | 726, 09 | ||
| 60, 464 | -26, 946 | 7640, 508 | 3655, 9 | ||
| 45, 124 | 60, 464 | 235, 3156 | 2036, 2 | ||
| 50, 244 | 45, 124 | 26, 2144 | 2524, 5 | ||
| 2, 361 | 50, 244 | 2292, 782 | 5, 574 | ||
| -59, 229 | 2, 361 | 3793, 328 | 3508, 1 | ||
| 41, 431 | -59, 229 | 10132, 44 | 1716, 5 | ||
| -68, 450 | 41, 431 | 12073, 83 | 4685, 4 | ||
| 69, 668 | -68, 45 | 19076, 58 | 4853, 6 | ||
| 36, 078 | 69, 668 | 1128, 288 | 1301, 6 | ||
| -34, 263 | 36, 078 | 4947, 856 | |||
| -50, 143 | -34, 263 | 252, 1744 | 2514, 3 | ||
| Сумма | -0, 002 | 50, 141 | 84921, 85 | 37911, 97 |
3. На основе данных о валовом внутреннем продукте (ВВП) необходимо выполнить следующие операции:
- доказать с помощью теста Дики-Фуллера, что изучаемый временной ряд является стационарным;
- построить автокорреляционную функцию и сделать вывод о наличии тенденции автокорреляции в остатках;
- в случае отсутствия автокорреляции построить аддитивную модель временного ряда; в случае наличия автокорреляции построить модель авторегрессии;
- осуществить прогноз на четыре уровня вперед.
Исходный временной ряд приведен в таблице 6.6.
Решение задачи разобьем на этапы:
а) докажем стационарность временного ряда с помощью теста Дики-Фуллера (см. формулу 6.32). Исходные данные теста представлены в таблице 6.5.
Таблица 6.6 - Информация периода наблюдения
| Год | квартал | ВВП | Год | квартал | ВВП |
| I | 1900, 9 | I | 3516, 8 | ||
| II | 2105, 0 | II | 3969, 8 | ||
| III | 2487, 9 | III | 4615, 2 | ||
| IV | 2449, 8 | IV | 4946, 4 | ||
| I | 2259, 5 | I | 4479, 2 | ||
| II | 2525, 7 | II | 5172, 9 | ||
| III | 3009, 2 | III | 5871, 7 | ||
| IV | 3023, 1 | IV | 6096, 2 | ||
| I | 2850, 7 | I | 5661, 8 | ||
| II | 3107, 8 | II | 6325, 8 | ||
| III | 3629, 8 | III | 7248, 1 | ||
| IV | 3655, 0 | IV | 7545, 4 | ||
| I | 6566, 2 | ||||
| II | 7647, 5 |
Таблица 6.5 - Исходные данные теста Дики-Фуллера
| Yt | t | Yt-1 | Yt | t | Yt-1 |
| - | 3969, 8 | 3516, 8 | |||
| 1900, 9 | 4615, 2 | 3969, 8 | |||
| 2487, 9 | 4946, 4 | 4615, 2 | |||
| 2449, 8 | 2487, 9 | 4479, 2 | 4946, 4 | ||
| 2259, 5 | 2449, 8 | 5172, 9 | 4479, 2 | ||
| 2525, 7 | 2259, 5 | 5871, 7 | 5172, 9 | ||
| 3009, 2 | 2525, 7 | 6096, 2 | 5871, 7 | ||
| 3023, 1 | 3009, 2 | 5661, 8 | 6096, 2 | ||
| 2850, 7 | 3023, 1 | 6325, 8 | 5661, 8 | ||
| 3107, 8 | 2850, 7 | 7248, 1 | 6325, 8 | ||
| 3629, 8 | 3107, 8 | 7545, 4 | 7248, 1 | ||
| 3629, 8 | 6566, 2 | 7545, 4 | |||
| 3516, 8 | 7647, 5 | 6566, 2 |
В таблице yt – зависимая переменная; t, yt-1 – независимые переменные регрессионной модели. По описанной в третьей главе последовательности регрессионного анализа находим постоянные коэффициенты модели: r=0, 378. Так как значение коэффициента r принадлежит интервалу (0; 1), то изучаемый временной ряд является стационарным.
б) Исследуем временной ряд с помощью автокорреляционной функции (рис. 6.5, 6.6). На рисунках показаны: исходный ряд (сверху) и автокорреляционная функция (АКФ) до лага 9 (снизу). На нижней диаграмме штриховой линией обозначен уровень «белого шума» - граница статистической значимости коэффициентов корреляции.

Рис. 6.5. Линейная модель тренда,
построенная по исходным данным
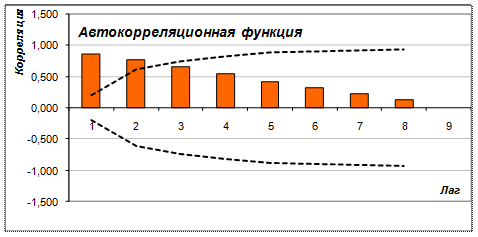
Рис. 6.6. Выборочная автокорреляционная функция
Если значения коэффициентов автокорреляции превышают уровень «белого шума», то коэффициент является статистически значимым. Автокорреляционная функция была построена с помощью одноименной надстройки программного продукта Microsoft Excel.
Если бы все коэффициенты автокорреляции были незначимы, что ряд был бы не пригоден для прогнозирования. Таким образом, имеется сильная корреляция 1 и 2 порядка, соседних членов ряда, но и удаленных на 1 единицу времени друг от друга. Корреляционные коэффициенты значительно превышают уровень «белого шума». По графику автокорреляции видим наличие четкого тренда.
Наличие сезонных колебаний позволяет выявить внутренняя динамика ряда. На первом этапе необходимо найти первую разность его членов, т.е. для каждого квартала найти изменение значения по сравнению с предыдущим кварталом (табл. 6.6).
Таблица 6.6 - Первая разность уровней временного ряда
| Год | квартал | ВВП | Год | квартал | ВВП |
| I | - | I | -138, 2 | ||
| II | 204, 1 | II | 453, 0 | ||
| III | 382, 9 | III | 645, 4 | ||
| IV | -38, 1 | IV | 331, 2 | ||
| I | -190, 3 | I | -467, 2 | ||
| II | 266, 2 | II | 693, 7 | ||
| III | 483, 5 | III | 698, 8 | ||
| IV | 13, 9 | IV | 224, 5 | ||
| I | -172, 4 | I | -434, 4 | ||
| II | 257, 1 | II | 664, 0 | ||
| III | 522, 0 | III | 922, 3 | ||
| IV | 25, 2 | IV | 297, 3 | ||
| I | -979, 2 | ||||
| II | 1081, 3 |
Для первой разности построим автокорреляционную функцию (рис. 6.8). По графику 6.8 можно видеть, что первые разности возрастают, т.к. тренд восходящий. Видна автокорреляция 2 и 4-го порядков, что говорит о полугодовой и годовой сезонности. Если бы сезонность не была выявлена, то прогноз осуществлялся бы аддитивной моделью тренда. В данном случае обосновано применение авторегрессионной модели прогнозирования.
в) построим авторегрессионную модель. Так как АКФ экспоненциально убывает, то порядок авторегрессионной модели p будет равен 2, тогда авторегрессионная модель (6.10) примет вид:
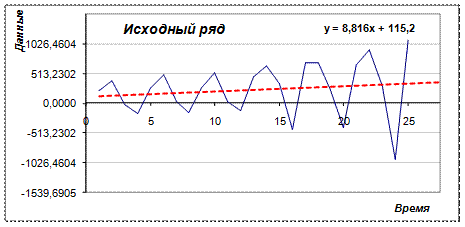
Рис. 6.7. Исходный ряд частот
(первых разностей уровней временного ряда)
Исходные данные для проведения регрессионного анализа приведены в таблице 6.7.
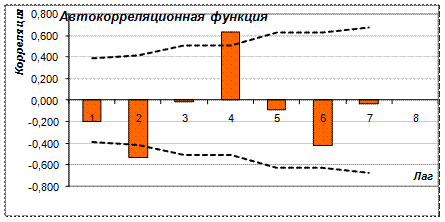
Рис. 6.8. Частотная выборочная автокорреляционная функция

Таблица 6.7 - Исходные данные для нахождения коэффициентов авторегрессионной модели при p=2
| t | Yt | Yt-1 | Yt-2 | t | Yt | Yt-1 | Yt-2 |
| - | - | 3969, 8 | 3516, 8 | ||||
| - | 4615, 2 | 3969, 8 | 3516, 8 | ||||
| 2487, 9 | 1900, 9 | 4946, 4 | 4615, 2 | 3969, 8 | |||
| 2449, 8 | 2487, 9 | 4479, 2 | 4946, 4 | 4615, 2 | |||
| 2259, 5 | 2449, 8 | 2487, 9 | 5172, 9 | 4479, 2 | 4946, 4 | ||
| 2525, 7 | 2259, 5 | 2449, 8 | 5871, 7 | 5172, 9 | 4479, 2 | ||
| 3009, 2 | 2525, 7 | 2259, 5 | 6096, 2 | 5871, 7 | 5172, 9 | ||
| 3023, 1 | 3009, 2 | 2525, 7 | 5661, 8 | 6096, 2 | 5871, 7 | ||
| 2850, 7 | 3023, 1 | 3009, 2 | 6325, 8 | 5661, 8 | 6096, 2 | ||
| 3107, 8 | 2850, 7 | 3023, 1 | 7248, 1 | 6325, 8 | 5661, 8 | ||
| 3629, 8 | 3107, 8 | 2850, 7 | 7545, 4 | 7248, 1 | 6325, 8 | ||
| 3629, 8 | 3107, 8 | 6566, 2 | 7545, 4 | 7248, 1 | |||
| 3516, 8 | 3629, 8 | 7647, 5 | 6566, 2 | 7545, 4 |
Зачеркнутые числа не участвует в построении модели авторегрессии. Зависимыми переменными являются yt-1 и yt-2. С помощью программного продукта Excel был проведен регрессионный анализ и были найдены постоянные коэффициенты модели:
yt=243, 017+0, 766yt-1+0, 241yt-2.
Таким образом,
y27=247, 017+0, 766*7647, 5+0, 241*6566, 2= 7687, 5;
y28=247, 017+0, 766* 7687, 5+0, 241*7647, 5=7978, 7;
y29=247, 017+0, 766* 7978, 7+0, 241* 7687, 5=8211, 4;
y30=247, 017+0, 766* 8211, 4+0, 241* 7978, 7=8459, 8.
6. Исходный временной ряд приведен в таблице 6.8.
Таблица 6.8 - Информация периода наблюдения
| Годы | |||||||||
| Динамика производства продукции | 10, 0 | 11, 1 | 12, 1 | 12, 5 | 13, 7 | 13, 9 | 19, 6 | 15, 9 | 19, 0 |
Необходимо осуществить прогноз методами экспоненциального сглаживания и гармонических весов Хельвига. Данный временной ряд нестационарен, что можно доказать с помощью теста Дики-Фуллера. Опишем процедуру экспоненциального сглаживания. Сглаженные данные получим с помощью уравнения (6.14). Пусть параметр сглаживание α равен 0, 8, т.е. фактор затухания (1-α) равен 0, 2. Тогда процесс экспоненциального сглаживания имеет вид
у2* = 0, 8*10+0, 2*10=10;
у3* = 0, 8*11, 1+0, 2*10=10, 88;
у4* = 0, 8*12, 1+0, 2*10, 88=11, 856;
у5* = 0, 8*12, 5+0, 2*11, 856=12, 3712;
у6* = 0, 8*13, 7+0, 2*12, 3712=13, 434;
у7* = 0, 8*13, 9+0, 2*13, 434=13, 607;
у8* = 0, 8*19, 6+0, 2*13, 607=18, 401;
у9* = 0, 8*15, 9+0, 2*18, 401=16, 4;
у10* = 0, 8*19, 0+0, 2*16, 4=18, 48.
Таким образом, получен прогноз на 10-е наблюдение.
Процедура экспоненциального сглаживания может быть осуществлена программными средствами Excel: Сервис®Анализ данных®Экспоненциальное сглаживание (рис. 6.9).
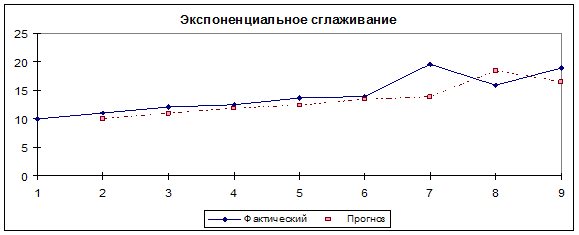
Рис. 6.9. Экспоненциальное сглаживание уровней временного ряда с фактором затухания 0, 2
Далее представим процедуру сглаживания уровней временного ряда методом гармонических весов Хельвига. Находим параметры уравнений отдельных фаз движения скользящего тренда.
Примем k=3, тогда получим (9-3+1) = 7 уравнений:
Y1(t)=8, 97+1, 05t, t=1, 2, 3;
Y2(t)=9, 8+0, 7t, t=2, 3, 4;
Y3(t)=9, 57+0, 8t, t=3, 4, 5;
Y4(t)=9, 87+0, 7t, t=4, 5, 6;
Y5(t)=11, 4+0, 45t, t=5, 6, 7;
Y6(t)=7, 8+1, 0t, t=6, 7, 8;
Y7(t)=-1, 1+2, 2t, t=7, 8, 9.
Далее по выделенным фазам были рассчитаны автокорреляционные функции, значения которых показали, что величина автокорреляционных функций уменьшается, то есть выполняется одно из основных условий применения метода гармонических весов для прогнозирования социально-экономических явлений.
С помощью полученных уравнений определяем значение скользящего тренда. При t=1 имеем одно значение Y*1(t), которое получаем из уравнения Y1(t)=8, 97+1, 05·1=10, 02.
При t=2 имеем два значения Y*2(t), которые получим из уравнений
Y2(t)=8, 97+1, 05·2=11, 07; Y2(t)=9, 8+0, 7·2=11, 2.
Отсюда Y*2(t) = (11, 07+11, 2): 2=11, 13
Аналогично находим все значения Y*j(t).
Y* 3(t) = 11, 99; Y* 4(t) = 12, 68; Y* 5(t) = 13, 53;
Y* 6(t) = 13, 99; Y* 7(t) = 14, 55; Y* 8(t) = 16, 15; Y* 9(t) = 18, 74
Затем были рассчитаны приросты:
w2 = 1, 11; w3 = 0, 86; w4 = 0, 70; w5 = 0, 85; w6 = 0, 46; w7 = 0, 56; w8 = 1, 6; w9 = 2, 59.
Гармонические веса определялись по формуле 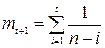 :
:
m2 = 0, 125; m3 = 0, 268; m4 = 0, 435; m5 = 0, 635; m6 = 0, 885; m7 = 1, 218; m8= 1, 717; m9= 2, 717.
Гармонические коэффициенты, полученные по формуле 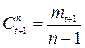 составили: С2 = 0, 0156; С3 = 0, 0335; С4 = 0, 0543; С5 = 0, 0793; С6 = 0, 1106; С7 = 0, 1522; С8 = 0, 2147; С9 = 0, 3397.
составили: С2 = 0, 0156; С3 = 0, 0335; С4 = 0, 0543; С5 = 0, 0793; С6 = 0, 1106; С7 = 0, 1522; С8 = 0, 2147; С9 = 0, 3397.
Все эти коэффициенты удовлетворяют необходимым условиям. Используя формулу  , находим средний абсолютный прирост
, находим средний абсолютный прирост 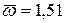 и рассчитываем прогнозные значения производства реализованной продукции; полученные данные вносим в таблицу 6.9. Доверительные интервалы прогноза находятся с применением неравенства Чебышева для случайной величины
и рассчитываем прогнозные значения производства реализованной продукции; полученные данные вносим в таблицу 6.9. Доверительные интервалы прогноза находятся с применением неравенства Чебышева для случайной величины  .
.
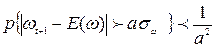 , (6.37)
, (6.37)
здесь 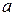 – заданное целое положительное число,
– заданное целое положительное число, 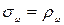 , где
, где
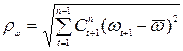 . (6.38)
. (6.38)
Значения переменной 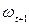 коррелированны между собой. Поэтому можно предположить, что прогнозная величина
коррелированны между собой. Поэтому можно предположить, что прогнозная величина 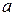 переменна. Она является функцией отдаленности от l, где l = 1, 2, 3, ……t-1. Функция
переменна. Она является функцией отдаленности от l, где l = 1, 2, 3, ……t-1. Функция 
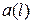 определяется из формулы:
определяется из формулы:
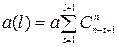 . (6.39)
. (6.39)
Тогда доверительные интервалы для предсказанных значений yt+1 следующие:
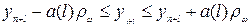 . (6.40)
. (6.40)
В примере значение 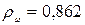 тыс. руб., значение
тыс. руб., значение 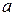 примем равным 4, а значение
примем равным 4, а значение 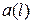 найдем по формуле (6.39). Все расчеты объединим в таблице 6.9.
найдем по формуле (6.39). Все расчеты объединим в таблице 6.9.
Таблица 6.9 - Прогноз производства реализованной продукции
Годы
| 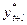
| 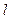
| 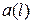
| 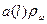
| Доверительный интервал | |
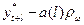
| 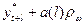
| |||||
| 20, 25 | 2, 218 | 1, 913 | 18, 4 | 22, 16 | ||
| 21, 76 | 2, 826 | 2, 437 | 19, 32 | 24, 20 | ||
| 23, 27 | 3, 269 | 2, 819 | 20, 45 | 26, 09 |
|
|