Теория приближенных (неточных, грубых) множеств (rough sets)

Теория приближенных множеств (rough sets) была разработана [Zdzisł aw Pawlak, 1982] как новый математический подход для описания неопределенности, неточности и неуверенности. Она основана на утверждении, что с каждым объектом универсума мы связываем некоторую информацию (данные, знания). Объекты, характеризуемые одинаковой информацией, являются неразличимыми (сходными) с точки зрения имеющейся о них информации. Отношение неразличимости, порождаемое таким способом, является математической основой теории приближенных (грубых) множеств.

Основой концепции теории приближенных множеств являются операции аппроксимации множеств.

Дадим теперь понятие аппроксимации приближенных множеств:

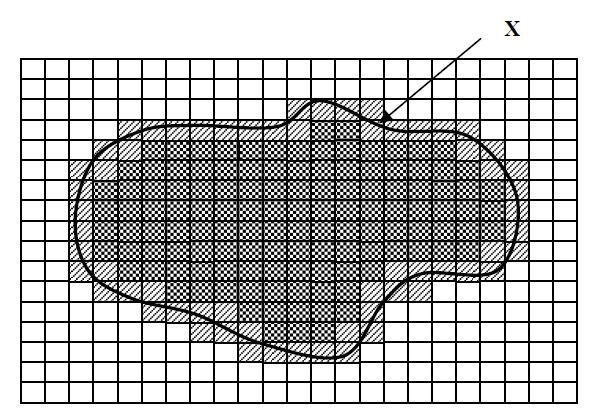
· Нижняя аппроксимация множества Х включает в себя элементы, которые действительно принадлежат множеству Х.

· Верхняя аппроксимация множества Х + включает в себя элементы, которые возможно принадлежат множеству Х.

· Граница (разница между верхней и нижней аппроксимацией) представляет собой область неразличимости.