Рассуждения с нечеткими множествами

Понятие нечеткого множества - эта попытка математической формализации нечеткой информации для построения математических моделей. В основе этого понятия лежит представление о том, что составляющие данное множество элементы, обладающие общим свойством, могут обладать этим свойством в различной степени и, следовательно принадлежать к данному множеству с различной степенью. При таком подходе высказывания типа “такой-то элемент принадлежит данному множеству” теряют смысл, поскольку необходимо указать “насколько сильно” или с какой степенью конкретный элемент удовлетворяет свойствам данного множества.

Определение 1. Нечетким множеством (fuzzy set) 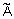на универсальном множестве U называется совокупность пар (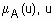), где 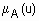- степень принадлежности элемента к нечеткому множеству 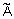. Степень принадлежности - это число из диапазона [0, 1]. Чем выше степень принадлежности, тем в большей мерой элемент универсального множества соответствует свойствам нечеткого множества.

Определение 2. Функцией принадлежности(membership function) называется функция, которая позволяет вычислить степень принадлежности произвольного элемента универсального множества к нечеткому множеству.

Если универсальное множество состоит из конечного количества элементов 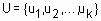, тогда нечеткое множество 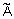записывается в виде 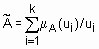. В случае непрерывного множества U используют такое обозначение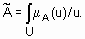

Примечание: знак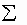и и 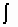в этих формулах означают совокупность пар 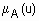и u.

При помощи нечетких множеств можно формально определить неточные и многозначные понятия, такие как «высокая температура», «молодой человек», «средний рост» либо «большой город». Перед формулированием определения нечеткого множества необходимо задать так называемую область рассуждений (universe of discourse). В случае неоднозначного понятия «много денег» большой будет признаваться одна сумма, если мы ограничимся диапазоном [0, 1000 руб] и совсем другая - в диапазоне [0, 1000000 руб]. Область рассуждений, называемая в дальнейшем пространством или множеством, будет чаще всего обозначаться символом 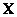. Необходимо помнить, что 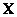- четкое множество.

Каждое слово - нечеткая переменная.

Вместе - нечеткий терм.

Используются интервальные исчисления.

Для обработки экспертных знаний - лучший вариант.

20. Теория Демпстера–Шефера

Подход, принятый в теории Демпстера-Шефера (ТДШ) отличается от байесовского подхода и метода коэффициентов уверенности тем, что, во-первых, здесь используется не точечная оценка уверенности (коэффициент уверенности), а интервальная оценка. Такая оценка характеризуется нижней и верхней границей, что более надежно. Во-вторых, ТДШ позволяет исключить взаимосвязь между неопределенностью (неполнотой знаний) и недоверием, которая свойственна байесовскому подходу.

В рамках ТДШ множеству высказываний А приписывается диапазон значений [Bl(А), Р1(А)], в котором находятся степени доверия (правдоподобия) каждого из высказываний. Здесь В1(А) -степень доверия к множеству высказываний, изменяющая свои значения от 0 (нет свидетельств в пользу А)до 1 (множество высказываний А истинно); Р1(А) -степень правдоподобия множества высказываний А, определяемая с помощью формулы: Pl(A) = 1-Bl(not A)

Предположим, что существуют две конкурирующие гипотезы h1 и h2. При отсутствии информации, поддерживающей эти гипотезы, мера доверия и правдоподобия каждой их них принадлежат отрезку [0; 1]. По мере накопления эти интервалы будут уменьшатся, а доверие гипотезам – увеличиваться. В теории Демпстера-Шефера неопределенность знаний представляется с помощью некоторого множества X. Элементы этого множества соответствуют возможным фактам или заключениям. Неопределенность состоит в том, что заранее неизвестно, какое из возможных значений примет факт или заключение х? X. Для характеристики степени определенности в ТДШ вводится некоторая единичная мера уверенности (ее называют также единичной массой уверенности), которая распределяется между элементами X. При этом, если вся масса (степень) уверенности приходится на один элемент х? X, то никакой неопределенности нет. Неопределенность возникает, когда масса уверенности распределяется между несколькими элементами х? X. Распределение масс уверенности (Рисунок 6.2) между элементами множества X, представлено в виде точек [64].Здесь Х= { х1, х2, х3 }.

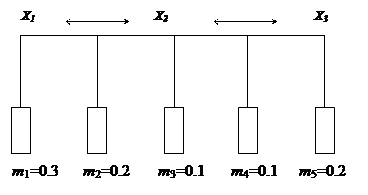
Рисунок 6.2 Распределение масс уверенности

С каждым элементом множества X жестко связана соответствующая масса уверенности. Так, х 1 соответствует m 1= 0, 3 x 2- m 2= 0, 1 x 3- m 3= 0, 2. Имеются также свободные массы уверенности m 4= 0, 2 m 5= 0, 2, которые относятся сразу к нескольким элементам. Масса m 4 свободно перемещается между элементами x 1 и x 2, а масса m 5 - между элементами x 2 и x 3, т.е. m 4 закреплена за подмножеством { x 1, x 2}, а m 5 - за подмножеством { x 2, x 3, }. Массы выражают степень уверенности в возможных значениях фактов или заключений. Так, степень уверенности в значении х 1 может изменяться от 0, 3 до 0, 5. Таким образом, степень незнания соответствует массе, местоположение которой не определено.

В общем случае распределение масс уверенности задается функцией m(А), обладающей следующими свойствами:

m(?)=0,

? m(А)=1,

Здесь А - множество, образованное из подмножеств X, которым назначены соответствующие массы (степени) уверенности; m(А) - функция, которая задает отображение А на интервал [0, 1]. Для примера (Рисунок 6.2) имеем:

А = {?, {х1}, {х2}, {х3}, {х1, х2}, {х2, х3}, {х1, х3}},

а распределение масс уверенности задаётся функцией m(А), характеризуемой множеством значений:

т(А) = { 0; 0, 3; 0, 1; 0, 2; 0, 2; 0, 2; 0 }.

Обратим внимание, что А состоит из подмножеств. Обозначим каждое такое подмножество через Аi. Степень доверия к высказываниям, соответствующим подмножеству Аi, может быть вычислена по формуле

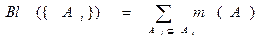
Теория Демпстера—Шефера разработана для того, чтобы можно было учесть различие между неопределенностью (uncertainty) и незнанием (ignorance). Вместо вычисления вероятности высказывания в ней вычисляется вероятность того, что данное свидетельство поддерживает высказывание. Этот показатель измерения степени уверенности называется доверительной функцией (belief function), которая обозначается как Bel (X).

Вернемся к задаче с подбрасыванием монеты, чтобы рассмотреть пример применения доверительных функций. Предположим, что к вам подходит подозрительный тип и предлагает поспорить на 10 долларов, что его монета упадет орлом вверх после следующего подбрасывания. С учетом того, что эта монета может оказаться либо подлинной, либо фальшивой, какую степень уверенности вы должны назначить тому событию, что она упадет орлом вверх? В теории Демпстера—Шефера утверждается, что у вас пока нет свидетельств в пользу того или иного предположения, поэтому вам следует исходить из предположения, что степень уверенности Bel (Heads) =0 и что 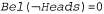. Таким образом, в системах формирования рассуждений на основе теории Демпстера—Шефера принят скептический взгляд на то, что могут подсказывать некоторые интуитивные соображения. А теперь предположим, что вы пригласили эксперта, который освидетельствовал монету и с определенностью 90% заявил, что монета является подлинной (т.е. он на 90% уверен, что Ρ {Heads) =0.5). В таком случае теория Демпстера-Шефера дает оценку Bel (Heads) = 0. 9x0.5 = 0.45 и, аналогичным образом, 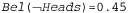. Таким образом, все еще остается " зазор" в 10%, который не охватывается этим свидетельством. В " правиле Демпстера" [382] показано, как комбинировать свидетельства для получения новых значений Bel, а в работе Шефера эти вычисления развиты до уровня полной вычислительной модели.

Рассмотрим двух возможных игроков

Первая игра — подбрасывание монеты, где ставки делаются на то, выпадет орел или решка. Теперь представим вторую игру, в которой ставки принимаются на исход боя между лучшим в мире боксёром и лучшим в мире борцом. Предположим, мы несведущи в боевых искусствах, и нам весьма трудно определиться на кого ставить.

Многие люди будут менее уверены в ситуации второй игры, в которой вероятности неизвестны, чем в первой игре, где легко увидеть, что вероятность каждого исхода равна половине. В случае второй игры, Байесовская теория присвоит каждому исходу половинную вероятность, вне зависимости от информации, делающей один из исходов более вероятным, чем другой. Теория Демпстера-Шафера позволяет определить степень уверенности, которую имеет игрок, относительно вероятностей присвоенных различным исходам.

Формализация

Пусть 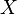— универсальное множество, набор всех рассматриваемых утверждений. Показательное множество, 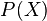, совокупность всех подмножеств множества 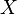, включая пустое множество, 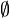. Например, если:

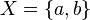
то

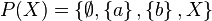
По определению, масса пустого множества — ноль:

Массы оставшихся элементов показательного множества нормированы на единичную сумму:

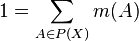
Масса элемента показательного множества, 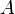, выражает соотношение всех уместных и доступных свидетельств, которые поддерживают утверждение, что определённый элемент 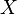принадлежит 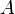но не принадлежит ни одному подмножеству 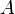. Величина относится только к множеству 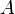и не создаёт никаких дополнительных утверждений о других подмножествах 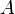, каждое из которых, по определению, имеет свою собственную массу.

Исходя из приписанных масс, могут быть определены верхняя и нижняя границы интервала возможностей. Этот интервал содержит точную величину вероятности рассматриваемого подмножества (в классическом смысле), и ограничена двумя неаддитивными непрерывными мерами, называемыми доверие (belief) (или поддержка (support)) и правдоподобие (plausibility):

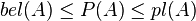
Доверие 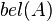к множеству 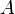определяется как сумма всех масс собственных подмножеств рассматриваемого множества:

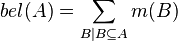
Правдоподобие 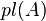— это сумма масс всех множеств 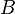пересекающихся с рассматриваемым множеством :

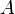Эти две меры соотносятся между собой следующим образом:

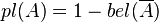
Из вышенаписанного следует, что достаточно знать хотя бы одну из мер (массу, доверие или правдоподобие), чтобы вычислить оставшиеся две.

Рассмотрим проблему объединения двух независимых множеств приписанных масс. Исходное правило объединения известное как правило комбинации Демпстера (en: Dempster's rule of combination) является обобщением правила Байеса. Это правило придаёт особое значение согласию между многочисленными источниками и игнорирует все конфликтующие свидетельства с помощью нормализации. Правомерность использования этого правила подвергается серьёзным сомнениям в случае значительных несоответствий между источниками информации.

Собственно, объединение (называемое присоединённая масса) вычисляется из двух множеств масс и 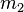следующим образом:

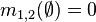
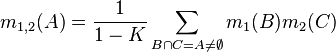
где:

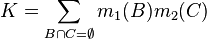
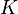является мерой конфликта между двумя наборами масс. Нормализирующий множитель, 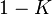, соответствует полному игнорированию несоответствий и приписыванию любой массе, соответствующей конфликту, пустого множества. Следовательно, эта операция приводит к контринтуитивным результатам в случае значительного конфликта при определённых обстоятельствах.

Шаферовский подход позволяет интерпретировать доверие и правдоподобие как границы интервала возможного значения истинности гипотезы:

доверие ≤ какая-то мера истинности ≤ правдоподобие.

Полагается, что:

Доверие к гипотезе = {сумма масс свидетельств, однозначно поддерживающих гипотезу}.

Правдоподобие = 1 − {сумма масс всех свидетельств, противоречащих гипотезе}.