
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Множества
|
|
Понятия «множество», «соответствие», «отношение» относятся к числу неопределяемых математических понятий. Поэтому для понятия множества дается описательное определение, содержание и смысл которого раскрываются при изучении теории множеств. Множество ― это набор, совокупность каких-либо объектов, называемых его элементами, обладающих некоторым общим для них характеристическим свойством. В качестве примеров можно привести множество действительных чисел, множество решений заданного алгебраического уравнения, множество прямых, проходящих через заданную точку. В принципе никаких ограничений на природу элементов, их количество и свойства не налагается, так что допустимо рассмотрение таких множеств, как множество налогоплательщиков, множество процентных ставок и т.п.
Понятие «множество» вводится для обозначения совокупности объектов (предметов), объединенных в одно целое либо путем перечисления, либо путем задания характеристического свойства Р(х) (одноместного предиката). Записывается множество так: X = { х │ Р (х) } и читается ― «множество тех х, для которых имеет место свойство Р».
Элементы, составляющие множество, обычно обозначаются малыми латинскими буквами, а само множество ― большой латинской буквой. Знак ∈ используется для обозначения принадлежности элемента множеству. Запись x ∈ A означает, что элемент x принадлежит множеству A. Если некоторый объект x не является элементом множества A, пишут x ∉ A. Например, если A ― это множество четных чисел, то 2∈ A, а 1∉ A.
П р и м е р 1: Запись Х = { х | х2 + 5х + 6=0 } означает, что X состоит из корней квадратного уравнения х2 + 5х + 6 = 0, решив его, множество X можно задать перечислением: X ={- 2, -3}.
О п р е д е л е н и е 1: Множество В называют подмножеством множества А, если 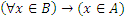 .
.
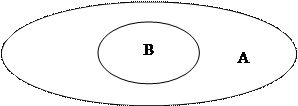 |
В этом случае пишут: 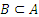 и читают «В ― подмножество А», или «В включено в А» или «В содержится в А».
и читают «В ― подмножество А», или «В включено в А» или «В содержится в А».
С количественной точки зрения, множества бывают конечные и бесконечные. Конечное множество содержит определенное количество элементов, которое можно сосчитать. Если же любое число, каково бы велико оно ни было, оказывается недостаточным, чтобы сосчитать элементы множества, то оно называется бесконечным. Конечное множество может содержать один элемент и даже ни одного элемента. Множество, не содержащее ни одного элемента, называют пустым и обозначают Ø. Принято считать, что Ø ⊂ А, где А ― любое множество, а также, что 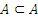 .
.
Количество элементов множества А обозначают 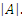 Если множество А конечно и содержит n элементов, то пишут:
Если множество А конечно и содержит n элементов, то пишут: 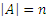 . Тот факт, что множество А бесконечно, записывают так:
. Тот факт, что множество А бесконечно, записывают так: 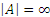 .
.
Множество, которое содержит в себе все мыслимые множества, называют универсальным и обозначают буквой U.
З а м е ч а н и е: следует четко различать обозначения ∈ и⊂, а также понятия: элемент множества и подмножество, состоящее из одного элемента.
Например: если А = {a, b, с}, то записи а ∈ А и { а }⊂ А ― правильны, а записи а ⊂ А и { a }∈ А ― неправильны.
О п р е д е л е н и е 2: (А = В)⇔ (А⊂ В)& (B⊂ A).
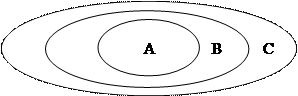
Для придания наглядности различным рассуждениям, связанным с множествами, используют диаграммы Эйлера-Венна.
Данный рисунок иллюстрирует тот очевидный факт, что если 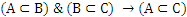 .
.
 |
Дадим определения основным теоретико-множественным операциям:
Пересечением множеств A и B называется множество, состоящее из всех тех и только тех элементов, которые принадлежат обоим этим множествам. Пишут: A∩ B. Множество A∩ B может быть задано с помощью характеристического свойства: A∩ B  { х │ х ∈ А & х ∈ В}. Изобразим A∩ B с помощью диаграммы Эйлера-Венна:
{ х │ х ∈ А & х ∈ В}. Изобразим A∩ B с помощью диаграммы Эйлера-Венна:
 |
Объединением множеств A и B называется множество, состоящее из всех тех и только тех элементов, которые принадлежат хотя бы одному из этих множеств. Записывают: A∪ B. Зададим множество A∪ B с помощью характеристического свойства: A∪ B  { х │ х ∈ А ⋁ х ∈ В}. Изобразим A∪ B с помощью диаграммы Эйлера-Венна:
{ х │ х ∈ А ⋁ х ∈ В}. Изобразим A∪ B с помощью диаграммы Эйлера-Венна:
 |
Разностью множеств A и B называется множество, состоящее из всех тех и только тех элементов, которые принадлежат A и не принадлежат B. Записывают: A\B. С помощью характеристического свойства: A\B  { х │ х ∈ А & х ∉ В}. Изобразим диаграмму Эйлера-Венна для множества A\B:
{ х │ х ∈ А & х ∉ В}. Изобразим диаграмму Эйлера-Венна для множества A\B:
 |
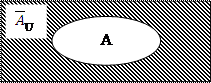
Дополнением множества A называют разность универсального множества U и множества A. Обозначение: 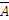 U или CA. С помощью характеристического свойства:
U или CA. С помощью характеристического свойства: 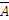 U
U  { х │ х ∉ А}. Проиллюстрируем множество
{ х │ х ∉ А}. Проиллюстрируем множество 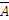 U на диаграмме Эйлера-Венна:
U на диаграмме Эйлера-Венна:
 |
Симметрической разностью (обозначение: A∆ B) множеств A и B называется объединение множеств A\B и B\A, т.е. A∆ B  (A\B)∪ (B\A). На диаграмме Эйлера-Венна:
(A\B)∪ (B\A). На диаграмме Эйлера-Венна:
 |
Так как любое множество объектов задается с помощью одноместного предиката Р(х) (характеристического свойства), то определенным выше теоретико-множественным операциям соответствуют логические операции: пересечению ― конъюнкция, объединению ― дизъюнкция, дополнению ― отрицание, т.е. операции над множествами служат своеобразными моделями логических операций (например, вместо конъюнкции двух одноместных предикатов (свойств) можно рассматривать соответствующую операцию пересечения множеств их истинности).
Из определения теоретико-множественных операций следует, что:
Если 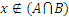 , то
, то 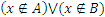 ;
;
Если 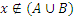 , то
, то 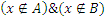 ;
;
Если 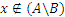 , то
, то 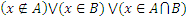
Если 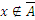 U, то
U, то 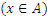 .
.
Принято теоретико-множественные операции выполнять в следующем порядке:
 ,
, 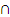 , ∪, \, ∆.
, ∪, \, ∆.
З а д а ч а: Доказать тождество:
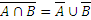 .
.
Д о к а з а т е л ь с т в о всех теоретико-множественных тождеств основано на понятии равенства двух множеств и определениях указанных операций. Поэтому для доказательства нужно установить, что
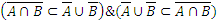 .
.
Покажем, что
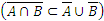 .
.
По определению подмножества, это включение будет выполняться, если
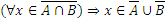 .
.
Пусть 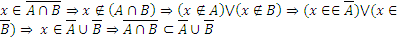 .
.
Теперь покажем, что
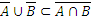 .
.
Для этого возьмем произвольный элемент y из множества 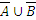 :
: 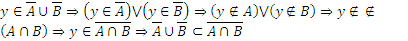 .
.
Из того, что 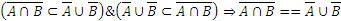 . Это доказательство может быть проиллюстрировано на диаграммах Эйлера-Венна:
. Это доказательство может быть проиллюстрировано на диаграммах Эйлера-Венна:
 |
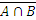
 |
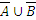
|
|