💸 Как сделать бизнес проще, а карман толще?

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое раписание, но и напоминать клиентам о визитах тоже. Проблема в том, что средняя цена по рынку за такой сервис — 800 руб/мес или почти 15 000 руб за год. И это минимальный функционал. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
⚡️ Для новых пользователей первый месяц бесплатно. А далее 290 руб/мес, это в 3 раза дешевле аналогов. За эту цену доступен весь функционал: напоминание о визитах, чаевые, предоплаты, общение с клиентами, переносы записей и так далее.
✅ Уйма гибких настроек, которые помогут вам зарабатывать больше и забыть про чувство «что-то мне нужно было сделать».
Сомневаетесь? нажмите на текст, запустите чат-бота и убедитесь во всем сами!

Электромагнитное поле. Уравнения Максвелла. Система уравнений электромагнитного поля.

В основе современной классической электродинамики лежит система уравнений Максвелла. Дифференциальная форма системы уравнений Максвелла в системе единиц СИ имеет вид:

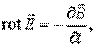
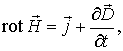
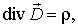
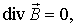
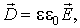
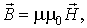
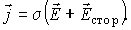
Приведенным уравнениям соответствуют интегральные формы записи:

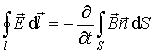
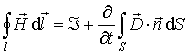
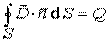
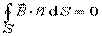
где 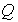- величина свободного заряда в объеме, охватываемом замкнутой поверхностью 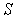, а величина " сила тока" 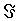определена соотношением

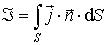
Наиболее последовательное представление о природе электромагнитного поля состоит в том, что система уравнений Максвелла принимается как постулат, как теоретическое обобщение всех известных экспериментальных законов электромагнетизма, как то целое, из которого как частные случаи следуют отдельные физические закономерности.

Особенно наглядно проявляется новизна представлений Максвелла о природе электромагнетизма в записи первого уравнения. В переменном векторном поле 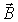частная производная по времени от вектора 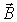не равна нулю. Это означает, что переменное векторное поле 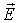, в отличие от электростатики, становится вихревым, оно перестает быть потенциальным!

При выяснении физического смысла второго уравнения оказывается, что в отсутствие объемной плотности тока проводимости 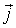магнитное поле может быть порождено переменным электрическим полем, это магнитное поле оказывается вихревым.

Рассматривая первое и второе уравнения совместно, замечаем, что переменное поле 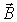порождает вихревое поле 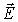, а переменное поле 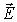порождает вихревое поле . Гениальность открытия Максвелла состоит в выявлении этой " симметрии" взаимодействия электрического и магнитного полей как единого электромагнитного поля.