
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Расчет коэффициентов автокорреляции на основе временного ряда потребления электроэнергии жителями региона
|
|
| t | yt | yt-1 | yt-2 | yt-3 | yt-4 | i (лаг) | ri |
| - | - | - | - | 0, 16515 | |||
| 4, 4 | - | - | - | -0, 56687 | |||
| 4, 4 | - | - | 0, 11356 | ||||
| 4, 4 | 0, 98303 | ||||||
| 7, 2 | 4, 4 | 0, 11871 | |||||
| 4, 8 | 7, 2 | 4, 4 | -0, 72205 | ||||
| 4, 8 | 7, 2 | -0, 00337 | |||||
| 4, 8 | 7, 2 | 0, 97385 | |||||
| 4, 8 | 7, 2 | 0, 09713 | |||||
| 5, 6 | 4, 8 | -0, 79985 | |||||
| 6, 4 | 5, 6 | -0, 08259 | |||||
| 6, 4 | 5, 6 | 0, 60667 | |||||
| 6, 4 | 5, 6 | - | - | ||||
| 6, 6 | 6, 4 | 5, 6 | - | - | |||
| 6, 6 | 6, 4 | - | - | ||||
| 10, 8 | 6, 6 | - | - |
Результаты расчетов, выполненные в таблице 9.2 наглядно показывают, что в данном ряду имеются ярко выраженные циклические колебания с длиной цикла равной 4. Четвертый, восьмой, двенадцатый коэффициенты корреляции на порядок превышают значения остальных коэффициентов.
На основе данных таблицы 9.2. построим коррелограмму (рис. 9.1).
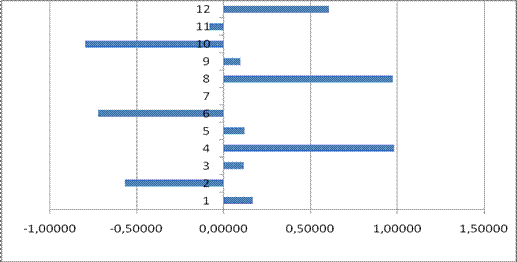
Рис. 9.1. Коррелограмма, построенная на основе данных таблицы 9.2
Эта коррелограмма позволяет наглядно наблюдать структуру ряда графически и подтверждает выводы, сделанные по результатам расчетов, выполненных в таблице 9.2.
Рассмотрим теперь, как выявить сезонную компоненту временного ряда и построить аддитивную или мультипликативную модель.
2й учебный вопрос. Выявление сезонной компоненты и построение аддитивной и мультипликативной модели временного ряда.
Следует иметь в виду, что с математической точки зрения между циклическими и сезонными колебаниями нет особой разницы. Различие лишь в содержательном смысле и длине цикла (периода колебаний). Сезонные колебания – это внутригодичные колебания, с длиной цикла меньше года, т.е. ежемесячные или ежеквартальные колебания. Циклические колебания как правило имеют длину цикла более года (например, цикл инвестиционной активности или колебания конъюнктуры рынка).
Существует несколько подходов к анализу структуры временных рядов, содержащих сезонные или циклические колебания. Моделирование циклических колебаний в целом осуществляется аналогично моделированию сезонных колебаний, поэтому мы рассмотрим здесь только методы моделирования последних. Простейший подход — расчет значений сезонной компоненты методом скользящей средней и построение аддитивной или мультипликативной модели временного ряда.
Построение аддитивной или мультипликативной модели временного ряда сводится к расчету значений T, S, E для каждого уровня ряда.
Процесс построения модели включает в себя следующие шаги:
1. Выравнивание исходного ряда методом скользящей средней;
2. Расчет значений сезонной компоненты S;
3. Устранение сезонной компоненты из исходных уровней ряда и получение выравненных данных (T+E) в аддитивной или (T*E) в мультипликативной модели;
4. Аналитическое выравнивание уровней (T+E) или (T*E) и расчет значений T c использованием полученного уравнения тренда;
5. Расчет полученных по модели значений (T+S) или (T*S)
6. Расчет абсолютных и/или относительных ошибок
Рассмотрим построение аддитивной модели ряда на том же примере, который был рассмотрен при расчете коэффициентов автокорреляции.
В таблице 9.3. приведен расчет оценок сезонной компоненты.
Таблица 9.3
|
|