Общий вид цепочек А-языков и КС-языков

Мы хотим получить характеристику цепочек А-языков, которая будет полезна для доказательства того, что некоторые языки не являются автоматными. Следующую теорему об общем виде цепочек А-языков называют теоремой о “разрастании”, потому что она в сущности говорит о том, что если дан А-язык и достаточно длинная цепочка в нем, то в этой цепочке можно найти непустую подцепочку, которую можно повторить сколько угодно раз (т.е. она “разрастается”), и все полученные таким образом “новые” цепочки будут принадлежать тому же А-языку. С помощью этой теоремы часто приводят к противоречию предположение о том, что некоторый язык является автоматным.

Теорема 5.1. Пусть L - А-язык. Существует такая константа p, что если y Î L и ½ y½ ³ p, то цепочку y можно записать в виде abg, где 0 < ½ b½ £ p и ab ⁱg Î L, для всех i ³ 0.

Доказательство. Если L - конечный язык, то положим константу p больше длины самой длинной цепочки языка L, тогда ни одна из цепочек языка не удовлетворяет условиям теоремы и она верна. В противном случае, пусть M = (Q, S, d, q₀, F) - конечный автомат с n состояниями и L(M) = L. Пусть p = n. Если y Î L и ½ y ½ ³ n, рассмотрим последовательность конфигураций, которую проходит автомат M, допуская цепочку y. Так как в этой последовательности, по крайней мере, n+1 конфигурация, то найдутся две конфигурации с одинаковыми состояниями. Поэтому, должна быть такая последовательность тактов, что (q ₀, abg) ú ¾ ^* (q ₁, bg) ú ¾ ^k (q ₁, g) ú ¾ ^* (q ₂, e), для некоторого q ₁ и 0 < k £ n. Отсюда 0 < ½ b½ £ n.

Но тогда, для любого i > 0 автомат может проделать следующую последовательность тактов:

(q ₀, ab ⁱ g) ú ¾ ^* (q ₁, b ⁱ g)

(q ₁, b ⁱ g) ú ¾ ⁺ (q ₁, b ^i-1 g)

..............

(q ₁, b ² g) ú ¾ ⁺ (q ₁, bg)

(q ₁, bg) ú ¾ ⁺ (q ₁, g)

(q ₁, g) ú ¾ ^* (q ₂, e).

Для случая i = 0 все еще очевиднее: (q ₀, ag) ú ¾ ^* (q ₁, g) ú ¾ ^* (q ₂, e)

Так как abg Î L, то и ab ⁱ g Î L, для всех i ³ 0. š

Эта теорема обычно используется для доказательства того, что некоторые выбранные цепочки не являются цепочками А-языка и, следовательно, не могут быть определены А-грамматиками.

Следствие 5.1. Язык L, состоящий из цепочек x ⁿ y ⁿ не является автоматным языком.

Допустим, что он автоматный. Тогда, для достаточно большого n цепочка x ⁿ y ⁿ может быть представлена в виде abg, причем b ¹ e и ab ⁱ g Î L, для всех i ³ 0.

Если b = x...x или b = y...y, то ag = ab ⁰ g Ï L, так как количество символов x и y в цепочке ag различно. Если b = x...xy...y, то abbg = ab ²g Ï L, так как в цепочке abbg символы x и y будут перемешаны. Полученное противоречие доказывает, что L - не является А-языком. š

Следствие 5.2. Язык арифметических выражений не является А-языком, так как он может содержать произвольное количество вложенных скобок, причем количество открывающих скобок совпадает с количеством закрывающих. Аналогично не является А-языком любой язык, содержащий вложенные конструкции типа фигурных скобок в языке C, begin - end, repeat - until и т.п. Каждая конечная А-грамматика, порождающая подобные конструкции, будет выводить и цепочки с неравным количеством открывающих и закрывающих скобок. Тем не менее анализировать подобные цепочки можно и с помощью автоматного подхода. При этом в синтаксисе языка допускается произвольное количество открывающих и закрывающих скобок, а контроль их парности возлагается на семантические подпрограммы. š

Прежде чем рассматривать теорему о разрастании КС-языков, примем без доказательств следующую теорему.

Теорема 5.2. Для любой КС-грамматики, которая не допускает вывода вида А Þ ⁺ aАb, где ½ a½ > 0 и ½ b½ > 0 можно построить эквивалентную А-грамматику. š

Иными словами любой язык, который при описании КС-грамматикой, не содержит самовставляемых нетерминалов, включает только одностороннюю рекурсию, при выводе наращивает цепочку в одну сторону, неважно, влево или вправо - является автоматным языком.

Теорема 5.3. Для любого КС-языка L существует постоянная p такая, что если y Î L и ½ y½ > p, то y = abgjl, где b¹ e, j¹ e и ab ⁱgj ⁱl Î L для любого i³ 0.

Доказательство. Аналогично с теоремой 5.1 рассмотрим только случай бесконечных языков.

Рассмотрим в бесконечном КС-языке L бесповторные деревья вывода, то есть такие, у которых ни на одной ветви нет повторяющихся нетерминалов. Таких деревьев конечное число. Максимальная высота бесповторного дерева v - равна количеству нетерминалов грамматики. Если максимальная длина правых частей правил грамматики равна b, то максимальная длина цепочки, выводимой бесповторными деревьями, будет не более b^v. Положим p = b^v. Рассмотрим цепочку с длиной больше p и ту ветвь ее дерева вывода, в которой нетерминалы повторяются.

Рассмотрим поддеревья D₁ и D₂, начинающиеся с повторяющегося нетерминала A. Если D₁ заменить на D₂, то получим дерево вывода цепочки agl. Подвеска дерева D₂ к корню D₁ возможна, так как после нее корень дерева D₁ соответствует применению того же правила, что и корень дерева D₂. Таким образом, полученное дерево вывода является деревом вывода в той же грамматике.

Если D₂ заменить на D₁, то получим дерево вывода цепочки ab ²gj ²l. Дерево D₁, которым заменяется D₂ содержит в себе D₂ в качестве поддерева. Заменив его на D₁, получим дерево вывода цепочки ab ³gj ³l. Продолжая такие замены, можно получить любую из цепочек ab ⁱgj ⁱl. š

Пример 5.1. Пусть дана КС-грамматика с правилами:

S ® aAp

A ® cAc ½ cbAb ½ d

Максимальная высота бесповторного дерева здесь равна 2, а максимальная длина цепочки, выводимая бесповторным деревом, равна 3 (бесповторно выводится только цепочка adp). На рис. 5.1 (а) показано дерево вывода цепочки acbdbp. Здесь принято следующее: a = a, b = cb, g = d, j = b, l = p. На рис. 5.1 (б) показана замена поддерева D₁ на D₂, а на рис. 5.1 (в) замена D₂ на D₁. †

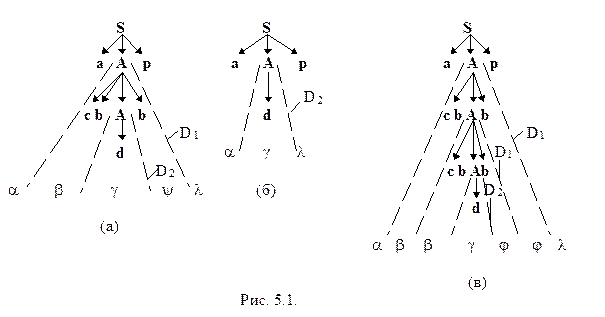
Теорема 5.3, как и теорема 5.1, чаще всего используется для доказательства того, что некоторые цепочки не принадлежат КС-языкам.

Следствие 5.3. Язык L, состоящий из цепочек x ⁿy ⁿz ⁿ, не является КС-языком.

Действительно, разделяя эту цепочку на пять частей abgjl любым возможным способом, мы увидим, что либо agl Ï L из-за неравного количества символов x, y и z; либо ab ²gj ²l Ï L из-за перемешивания символов внутри цепочки.

Следствие 5.4. Языки программирования в общем случае не являются КС-языками.

Например, в языках программирования каждая конкретная процедура имеет одно и то же число аргументов в каждом месте, где она упоминается. Можно показать, что такой язык не контекстно-свободен, отобразив множество программ с тремя вызовами одной и той же процедуры на не КС-язык { 0 ⁿ 10 ⁿ 10 ⁿ | n³ 0 }.

В этих языках встречаются и другие явления, характерные для не КС-языков. Так язык, требующий описания идентификаторов, длина которых может быть произвольно большой, до их использования, не контекстно-свободен. Правил КС-грамматик для описания таких явлений явно недостаточно.

Однако на практике все языки программирования считаются КС-языками. В компиляторах идентификаторы обычно обрабатываются лексическим анализатором и свертываются в лексемы прежде, чем достигают синтаксического анализатора. Контроль за их описанием до использования, также как и подсчет числа параметров в процедуре и т.п., возлагается на семантические подпрограммы, не входящие в собственно синтаксический анализ. Это позволяет существенно упростить синтаксис языков программирования.