
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Декомпозиция правил грамматики
|
|
Определение: две грамматики эквивалентны, если они порождают один и тот же язык. G1~G2, если L(G1)=L(G2).
Теорема: не существует алгоритма, определяющего эквивалентность или неэквивалентность двух грамматик, тем не менее существуют такие преобразования исходных грамматик, которые приводят к новым грамматикам, не выходящим из класса грамматик, эквивалентных исходным.
Критериями преобразования грамматик, приведения к эквивалентным грамматикам являются следующие: детерминированность; получение более короткого вывода цепочек; исключение тупиковых правил.
В предыдущей главе была сформулирована теорема о существовании для любой А-грамматики эквивалентной ей грамматики во вполне детерминированной форме и доказана первая часть теоремы, подтверждающая существование таких грамматик. Ниже будет доказана вторая часть теоремы, рассматривающая эквивалентность исходной А-грамматики и построенной.
Для доказательства эквивалентности исходной автоматной грамматики и построенной грамматики во вполне детерминированной форме необходимо доказать, что любая цепочка, принадлежащая языку L1, выводится и в грамматике G2 и наоборот: L1=L2, если L(G1) Ì L(G2) и L(G2) Ì L(G1).
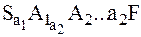 |
Рассмотрим произвольную цепочку φ =a1…ak Î L(G1), тогда существует вывод этой цепочки вида:
Согласно построению, если в исходной грамматике существует правило вида S→ aA1, то в преобразованной грамматике будет правило вида < S> → a<..A1…>.
Аналогично рассуждаем для произвольного шага: если Ai→ ai+1 Ai+1, то
<..Ai..> → ai+1<..Ai+1..>
На последнем шаге вывода, имея в исходной грамматике правило вида Ak-1→ akF, в преобразованной грамматике имеем правило <..Ak-1..> → ak<..F..>, то есть существует последовательность шагов вывода:
< S> a1 <..A1…>..ak<..F..> => φ Î L(G2)
В противоположную сторону рассуждения абсолютно аналогичны:
Пусть φ =a1…ak Î L(G2)=> существует вывод этой цепочки в языке, порождаемом грамматикой G2, то есть существует вывод цепочки: < S> a1 <..A1…>..ak<..F..>.
По построению, если существует правило вида < S> → a1<..A1…>, то в исходной грамматике существует правило вида S→ a1 A1.
Рассуждая аналогично, имея правило вида <..Ak-1..> → ak<..F..> в исходной грамматике, имеем правило вывода Ak-1→ akF, то есть φ Î L(G1) и => L(G2) Ì L(G1), откуда L1=L2. Что и требовалось доказать.
Следующие теоремы позволяют обосновать возможность эквивалентных преобразований, приводящих к грамматикам с большим количеством правил, но вывод в которых короче.
Пусть дана КС-грамматика G1=(VN, VT, R, S).
Теорема 4.1. Если в КС-грамматике G1 существуют правила Y®aXb и X®g, то грамматика G2=(VN, VT, R È { Y®agb}, S) эквивалентна G1.
Доказательство. Проверим, что любая цепочка, выводимая в одной грамматике, выводима и в другой.
Пусть j Î L(G1), тогда дерево вывода j в G1 является деревом вывода j и в G2. Обратно, пусть j Î L(G2), следовательно существует некоторое дерево вывода j в G2. Если при этом правило Y®agb не используется, то дерево вывода j в G2 является деревом вывода j в G1. Если же правило Y®agb использовалось при выводе j в G2, то фрагмент вывода Y Þ agb заменяем на фрагмент Y Þ aXb Þ agb.
В результате получим дерево, в котором используются правила только из P, то есть получим вывод цепочки в G1. Следовательно, из j Î L(G2) следует, что j Î L(G1).
Теорема 4.2. Пусть в грамматике G1 имеется множество правил
{Y® a Xb, X® g1, X® g2,..., X® gn}.
Тогда, заменив это множество на множество
{Y® ag1b, Y® ag2b,..., Y® agnb, X® g1, X® g2,... X® gn},
получим грамматику, эквивалентную G1. И далее, если X ¹ S и других правил, которые имеют X в правой части нет, то группу правил X® g k, 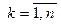 можно удалить.
можно удалить.
Доказательство. Многократно применяя теорему 4.1 в грамматику добавляем правила Y® agkb, где 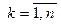 . Удаление правила Y® aXb не приводит к потере выводимых цепочек, так как фрагмент дерева вывода Y Þ aXb Þ agkb можно заменить на YÞ agkb.
. Удаление правила Y® aXb не приводит к потере выводимых цепочек, так как фрагмент дерева вывода Y Þ aXb Þ agkb можно заменить на YÞ agkb.
Пример 4.1. Рассмотрим фрагмент грамматики для описания числа
< число> ® < знак> < чбз>
< знак> ® + ½ -½ e.
Здесь в соответствии с теоремой 4.2: Y - < число>, a - пустая цепочка, X - < знак>, b - < чбз> (число без знака), g1 - +, g2 - -, g3 - e. Группу приведенных правил заменяем на правила
< число> ® + < чбз> ½ - < чбз> ½ < чбз>.
Теорема 4.3. Замена группы правил Y1® a 1Xb 1 , Y2® a 2Xb 2 ,... Ym® a mXbm, X® g на правила Y1® a 1gb 1 , Y2® a 2gb 2 ,... Ym® a mgb m, X® g, где других правил с нетерминалом X в левой части нет, приводит к эквивалентной грамматике. Если X ¹ S и других правил, которые имеют X в правой части нет, то правило X® g можно удалить.
Доказательство здесь аналогично теореме 4.2. ƒ
Пример 4.2. Замена правил:
S ® AB.C ½ AB. ½ A.C ½ B. ½ .C
A ® -
на правила:
S ® -B.C ½ -B. ½ -.C ½ B. ½ .C
приводят к эквивалентной грамматике.
Теорема 4.4. Декомпозиция правил. Замена в грамматике G1 группы правил
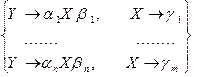 на группу правил
на группу правил 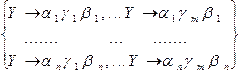 , если
, если
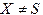 и других
и других 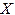 в левых и правых частях правил грамматики нет, приводит к грамматике, эквивалентной G1.
в левых и правых частях правил грамматики нет, приводит к грамматике, эквивалентной G1.
При декомпозиции n+m правил грамматики заменяется на n * m правил. ƒ
Пример 4.3. Рассмотрим КС - грамматику идентификатора, имеющую вид:
< И> ® < Б> ½ < Б> < И1>
< И1> ® < Б> ½ < Б> < И1> ½ < Ц> ½ < Ц> < И1>
< Б> ® a ½ b ½ c ½ ... ½ y ½ z
< Ц> ® 0 ½ 1 ½ 2 ½ ... ½ 8 ½ 9
В предложенной грамматике 42 правила. Проведем в ней декомпозицию по < Б> и по < Ц>. Получим новую грамматику, эквивалентную заданной.
< И> ® a ½ ... ½ z ½ a < И1> ½ ... ½ z < И1>
< И1> ® a ½ ... ½ z ½ a < И1> ½ ... ½ z < И1> ½ 0 ½...½ 9 ½ 0< И1> ½ ... ½ 9< И1>
В результате получено 4*26=104 правил для букв и 2*10=20 правил для цифр, итого 124 правила. Правил стало больше, но вывод, а следовательно и разбор, будет короче. Нетрудно видеть, что рассмотренная декомпозиция позволила перейти от КС-грамматики идентификатора к А-грамматике. ƒ
Отметим в заключении параграфа, что все рассмотренные теоремы работают в обе стороны. Так n * m правил при композиции можно заменить на n+m правил. Иногда лучше иметь правил поменьше и компактно описывать язык; иногда, с целью повышения эффективности разбора, их количество необходимо увеличить.
|
|