На дом. № 3956, 3958, 3960, 3966, 3988, 3990, 4000.

Линейным дифференциальным уравнением первого порядка называется уравнение, линейное относительно неизвестной функции 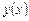и её производной первого порядка 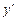. Оно имеет вид:

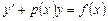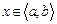, , (2.1)

где 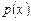и 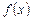-- известные функции независимой переменной 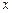, непрерывные на промежутке .

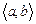Если 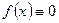, то уравнение (2.1) называется линейным однородным, исходное же уравнение (2.1) с правой частью 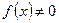называется линейным неоднородным дифференциальным уравнением. Однородное уравнение является уравнением с разделяющимися переменными и имеет общее решение такого вида:

.

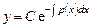Общее решение неоднородного уравнения можно найти методом вариации произвольной постоянной, который состоит в том, что решение ищется в виде

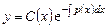, (2.2)

где -- неизвестная функция от 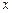. В результате подстановки (2.2) в уравнение (2.1) получаем дифференциальное уравнение, интегрируя которое, удаётся найти функцию .

Пример 2.1. Решить уравнение

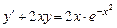. (2.3)

Решение. Однородное уравнение, соответствующее данному неоднородному, имеет вид: 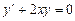, его общее решение 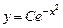, 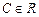. Общее решение уравнения (2.3) ищем в виде

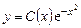, (2.4)

где - неизвестная функция. Подставляя (2.4) в (2.3), получаем уравнение 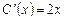, откуда .

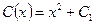В итоге, общее решение уравнения (2.3):

, .

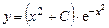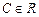Может оказаться, что дифференциальное уравнение линейно относительно 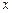как функции независимой переменной 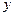, т.е. имеет такой вид:

.

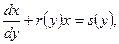
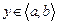Пример 2.2. .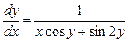

Решение. Данное уравнение является линейным относительно функции и её первой производной:

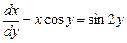. (2.5)

Сначала решаем соответствующее однородное уравнение

.

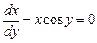Его общее решение имеет вид 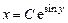, 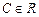. Решение уравнения (2.5) ищем в виде

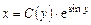, (2.6)

где 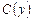- неизвестная функция. Подставляя (2.6) в (2.5), имеем:

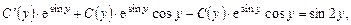
откуда

.

Интегрируя по частям, получим:

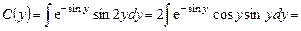
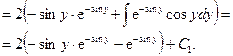
В итоге:

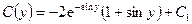. (2.7)

Подставляя (2.7) в (2.6), получаем общее решение исходного дифференциального уравнения:

.

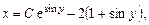
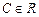3957. Решить уравнение

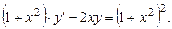
Решение. Разделим на 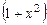левую и правую части уравнения. Поскольку 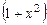не обращается в нуль нигде на оси ОX, никакие решения уравнения потеряны не будут. Получим:

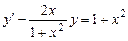. (2.8)

Однородное уравнение, соответствующее данному неоднородному:

.

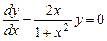Проинтегрируем, предварительно разделив переменные:

.

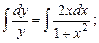
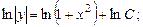
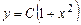Общее решение уравнения (2.8) ищем методом вариации постоянной, подставив в (2.8)

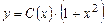, (2.9)

где C(x) - неизвестная функция, получим:

,

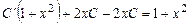откуда

; .

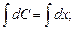
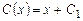Подставив в (2.9), получим общее решение исходного дифференциального уравнения:

,

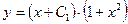3961. Решить уравнение .

Решение. Это уравнение становится линейным, если 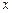считать функцией независимой переменной 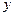. Тогда уравнение примет вид:

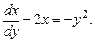(2.10)

Интегрируя соответствующее однородное уравнение, получаем:

.

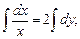
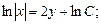
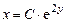Решение уравнения (2.10) ищем в виде

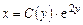. (2.11)

Подставив (2.11) в (2.10), получим:

;

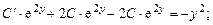
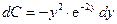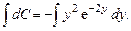
Интегрируя по частям дважды, имеем:

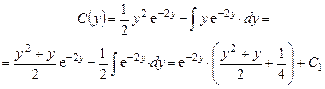
Зная 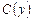, находим общее решение исходного дифференциального уравнения:

.

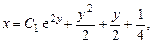
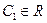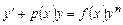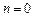Уравнение Бернулли имеет вид . При и 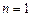оно является линейным, при других значениях 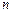приводится к линейному виду с помощью перехода к новой неизвестной функции .

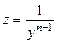Пример 2.3. Решить уравнение

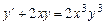. (2.12)

Решение. Разделив обе части уравнения на 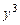, получим

.

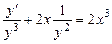При этом следует учесть, что 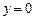является частным решением исходного уравнения. Сделав замену переменных 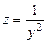, заметим, что 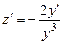. В результате уравнение (2.12) будет преобразовано к виду

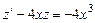. (2.13)

Решая однородное уравнение 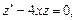находим

,

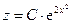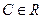
Подставив 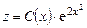в (2.13), получим ,

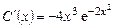откуда:

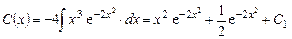и

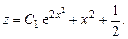
Общее решение исходного уравнения:

.

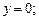
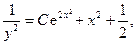
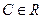4043. Решить уравнение Бернулли

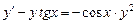
Разделив все на 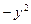получим:

.

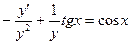Переходим к новой неизвестной функции 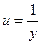, тогда 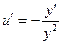и уравнение принимает вид

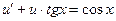(2.14)

Соответствующее однородное уравнение решаем методом разделения переменных:

.

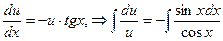
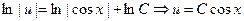Решение неоднородного уравнения ищем в виде

.

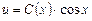После подстановки в (2.14) получаем уравнение

,

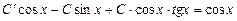из которого после сокращений получаем:

.

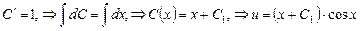Решение уравнения:

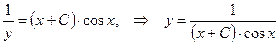
Контрольные вопросы.

1. Дайте определение линейного дифференциального уравнения первого порядка.
2. В каком случае линейное дифференциальное уравнение называется однородным, а в каком – неоднородным?
3. В чем состоит метод вариации произвольной постоянной?
4. Какой вид имеет уравнение Бернулли? Опишите метод решения уравнения Бернулли.