
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Стискаючі напруження, виникають в середині рідини, що знаходиться в спокої, називається гідростатичним тиском або напруженням гідростатичного тиску.
|
|
Розглянемо деякий об’єм рідкого тіла, що заходиться в рівновазі.
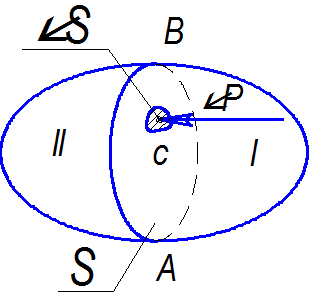
Поділимо площиною АВ даний об’єм рідини на дві частини. Рідина, заключна в І частині буде діяти на ІІ частину по площині АВ. Позначимо площину поділу через S уявно відкинувши верхню І частину. Тоді для збереження рівноваги нижньої частини замінимо на силу Р, що називається силою гідростатичного тиску яка діє на площу S. Поділив силу гідростатичного тиску Р на величину площі S, отримаємо середнє значення гідростатичного тиску.
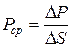
Візьмемо на площині АВ довільну точку С і виділимо навколо неї малу площину Δ S. На дану площу буде приходитись деяка сила Δ Р. Якщо ми будемо зменшувати дану площу Δ S до нуля ми отримаємо тиск в даній точці.
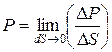
Властивості гідростатичного тиску. Гідростатичний тиск завжди спрямований вздовж внутрішньої нормалі до площадки, на яку вона діє.
Властивість доводиться від протилежного. Дійсно якщо припустити, що в якійсь точці рідини тиск направлений під кутом до площадки, то в цьому випадку його можна розкласти на нормальну та тангенціальну складову. Тангенціальна складова викличе зсув частинки рідини, що порушить рівновагу, рідина потече. Отже наше припущення, про те, що тиск направлений під кутом, не відповідає дійсності.
Теж саме можна припустити, що тиск направлений по внутрішній нормалі. Оскільки рідина не може витримувати розтягуючи зусиль, то рівновага у даному випадку знову буде порушена.
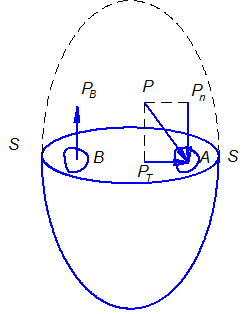
Таким чином, сила гідростатичного тиску, завжди направлена в середину рідини, і будуть силами стискаючими.

Друга властивість. Тиск в даній точці рідини по всіх напрямках однаковий, тобто величина тиску не залежить від кута нахилу площинки дії.
Якщо хоча б в одному з напрямків тиск змінить своє значення то спокій рідини обов’язково порушиться, рідина потече.
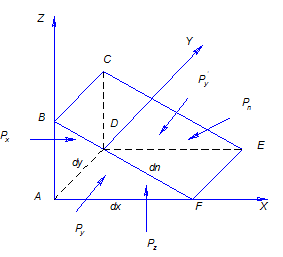
Ця властивість може бути доведена наступним чином: виділимо нескінченно малу призму із сторонами dx, dy, dz та dn. Розглянемо умови рівноваги під дією зовнішніх сил. Такими силами будуть сили гідростатичного тиску Px, Py Py’, Pz, Pn та масові (сила тяжіння, відцентрові сили) що діють на сторони призми. Сили Py Py’ рівні за величиною та протилежні за напрямком, тому вони зрівноважуються і не будуть прийматись до уваги.
Визначимо сили гідростатичного тиску Px, Pz, Pn.
Оскільки ділянки призми є нескінченно малими то середній гідростатичний тиск є одночасно і гідростатичним тиском в будь якій точці ділянки, тоді
Px= рxdydz, Pz= рzdxdy, Pn= рndydn.
Масові сили, що діють на призму можна визначити з залежності:
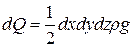
Співставивши масові сили з силами гідростатичного тиску бачимо, що вони є нескінченно малими. Тому в умовах нашого випадку цими силами можна знехтувати.
Для того, щоб призма знаходилась в рівновазі сума проекцій на любу вісь всіх сил, повинна дорівнювати нулю. Складемо умову рівноваги для вісі х, у оскільки сили Px , Pz паралельні осям координат то вони проецируються в натуральну величину.
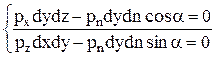
оскільки
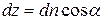 , а
, а 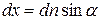 то
то
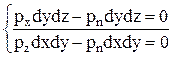 , або
, або 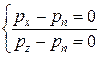 , то кінцева рівність:
, то кінцева рівність:
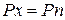 та
та  або
або 
Відповідно гідростатичний тиск в точці А по всіх напрямках однаковий, оскільки направлення нами було обрано довільно.
_________________________
Диференціальне рівняння рівноваги рідини (рівняння Ейлера)
Розглянемо загальний випадок спокою рідини. Для цього в просторі дослідної рідини оберемо систему координатних осей x, y, z з центром в точці 0 і фіксуємо довільну точку А з координатами x, y, z.
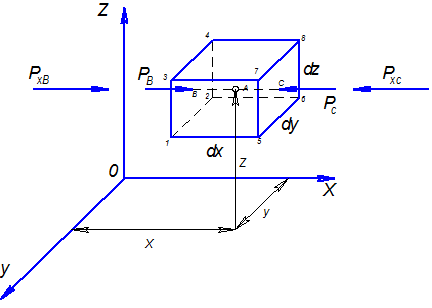
Тоді навколо точки А виділимо нескінченно малий паралелепіпед 1-2-3-4-5-6-7-8 з нескінченно малими сторонами dx, dy, dz, так щоб точка А знаходилась в центрі цього паралелепіпеда. Гідростатичний тиск, що виникає в точці А під дією зовнішніх сил, позначимо через р. Даний паралелепіпед буде в рівновазі в тому випадку, якщо сума проекцій всіх діючих сил на любу з координатних осей буде рівна нулю.
Зовнішніми силами, що діють на рідкий паралелепіпед є:
Поверхневі сили, обумовлені тиском сусідніх шарів рідини
І масові сили, пропорційні масі паралелепіпеда;
Так як масові сили різноманітні і вони можуть діяти на рідину в різній сукупності, то будемо вважати, що нам відомі одиничні проекції сумарних масових сил на координатні вісі і позначимо їх через X, Y, Z
Тоді проекція об’ємних сил 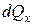 на вісь х буде рівна:
на вісь х буде рівна:
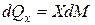 ;
;
де 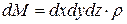
А значить і 
Аналогічно проекції на вісь Y, Z
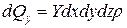 ,
, 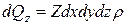
Х, Y, Z – мають розмірність прискорення і є проекціями прискорення на координатну вісь, та характеризують інтенсивність масової сили.
Розставимо сили гідростатичного тиску на грані 1-2-3-4 та 5-6-7-8 дані сили діють нормально до граней тобто направлені вздовж вісі х. Проведемо через точку А горизонтальну лінію ВС яка пересіче грань паралелепіпеда 1-2-3-4 в точці В, а грань 5-6-7-8 в точці С. Сили гідростатичного тиску позначимо через рс та рв
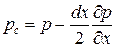 та
та 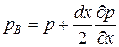
де частинна похідна 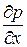 називається градієнтом гідростатичного тиску.
називається градієнтом гідростатичного тиску.
Тоді сили гідростатичного тиску на площадки РхВ та РхС:
 ,
, 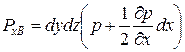 .
.
Спроектувавши на вісь х всі зовнішні сили, що діють на паралелепіпед, отримаємо
 .
.
Оскільки сили гідростатичного тиску РхВ та РхС є нормальними до граней 1-2-3-4 та 5-6-7-8 спроектуються на вісь х в натуральну величину. Проекції ж інших сил гідростатичного тиску, що діють на інші грані будуть рівні нулю і тому в рівняння не ввійдуть. Тоді рівняння можна записати як:
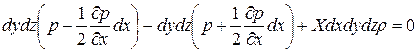
після нескладних перетворень отримаємо
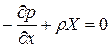
Аналогічно рівняння рівноваги відносно осей у та z:
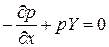
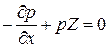
Отримані рівняння і є диференціальним рівнянням рівноваги рідини Ейлера.
Ці рівняння показують, що тиск в рідині залежить від інтенсивності масових сил. Це фізичний зміст рівняння.
Якщо рідина не стислива, то ці рівняння мають одну невідому величину – тиск р. Якщо рідина стислива, то ці рівняння мають дві невідомі величини – тиск р і густину 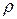 . І щоб система була замкнута потрібно додати рівняння стану газу
. І щоб система була замкнута потрібно додати рівняння стану газу 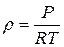 .
.
Загальне диференціальне рівняння рівноваги. Інтеграл Ейлера.
Помножимо диф. рівняння на dx, dy, dz і відповідно складемо:

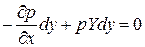
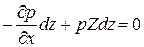
Додамо дану систему рівнянь:
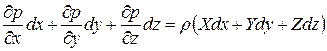 *
*
Ліва частина виразу є повним диференціалом тиску р.
Рівняння * може мати рішення тільки в тому випадку, якщо і права частина його теж буде повним диференціалом. А це можливо якщо існує якась силова функція 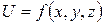 , котра залежить від координат і частинні похідні які дорівнюють проекціям одиничних масових сил. Цю функцію називають потенційною силовою функцією.
, котра залежить від координат і частинні похідні які дорівнюють проекціям одиничних масових сил. Цю функцію називають потенційною силовою функцією.
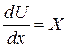 ,
, 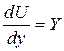 ,
, 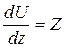
А сили, що відповідають цій функції називають силами, що мають потенціал (консервативні сили).
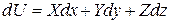
Отримане рівняння є загальним диференціальним рівнянням рівноваги, рішенням якої є інтеграл Ейлера.
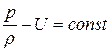
Інтеграл Ейлера показує, що в однорідній рідині тиск змінюється за таким же законом як і силова функція.
|
|