ЛЕКЦИЯ №2

по дисциплине «РАДИОАВТОМАТИКА»

Тема: Уравнения систем автоматического управления

Вопросы занятия:

1.Уравнения динамики и статики.

2. Линеаризация уравнений систем радиоавтоматики.

3. Пример линеаризации дифференциального уравнения САУ

Вопрос 1. Уравнения динамики и статики

Для исследования САУ или ее элементов необходимо получить математическое описание протекающих в них процессов.

Характер этих процессов определяется теми илиинымифизическими законами, математическая формулировка которых для данной системы (или элемента) и определяет уравнение, которому подчиняются рассматриваемые процессы.

Уравнения САУ и ее элементов могут быть:

1. Алгебраические (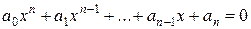, , 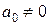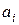-коэффициенты А.у., n – степень А.у.), квадратное кубическое.

2. Дифференциальные:

– обычные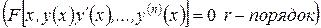

– в частных производных 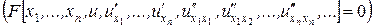функция 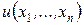удовлетворяющая этому соотношению т. е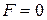

3. Интегродифференциональные уравнения;

4. Конечно – разностные;

В дальнейшем будем преимущественно рассматривать системы, описываемые дифференциальными уравнениями. Обычно уравнение системы получают, составляя уравнения отдельныхееэлементов.

Рассмотрим схему системы, изображенную на рис.1.

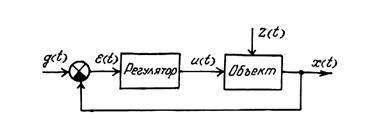
Рисунок 1

Предположим, что регулируемая величина х (t) может быть представлена ввиде

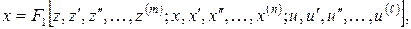(1)

а регулятор описывается двумя уравнениями

Уравнение (3) называют уравнением ошибки.

Система, представленная на рис.1, полностью описывается совокупностью уравнений (1), (2), (3).

Исключая в этих уравнениях " внутренние" переменные u (t) и , можно получить уравнение, связывающее регулируемую величину x (t) с внешними воздействиями g (t) и z (t):

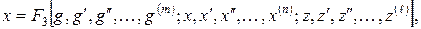(4)

Уравнение(4) определяет закон изменения во времени регулируемой величины под влиянием управляющих и возмущающих воздействий и называется уравнением динамики.

Допустим, что к системе в некоторый момент времени t ₀ приложены неизменные во времени (постоянные) воздействия g (t)= g ₀ и z (t)= z ₀. Если с течением времени выходной процесс системы стремится к некоторому установившемуся значению

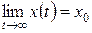(5)

тоиз (4) можно получить так называемое уравнение статики:

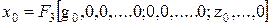. (6)

Статический режим можно описать графически, построивстатическую характеристику либоих семейство, если элементили система имеют несколько входов.

Семейство статических характеристик, соответствующее (6), может иметь вид, представленныйна рис.2.

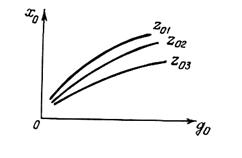
Рисунок 2

Статическую характеристику можно построить экспериментально, подавая на вход элемента или системы постоянную величину, после затухания переходных процессов.

Дифференциальное уравнение (4) может быть как линейным, так и нелинейным.

Вопрос 2. Линеаризация уравнений систем радиоавтоматики

Решение нелинейных дифференциальных уравнений высокого порядка представляет значительные трудности, поэтому стараются заменить в первом приближении нелинейное уравнение линейным.

Операция замены нелинейного дифференциального уравнения линейным называется линеаризацией.

Если функция F ₃ в (4) является аналитической, то линеаризацию можно произвести с помощью разложения в ряд Тейлора в окрестности точки, соответствующей некоторому заданному режиму системы. В частности, в системах стабилизации заданный режим соответствует постоянным значениям входных и выходных величин. В общем случае они должны изменятьсяпо определенному закону, однако из-за наличия возмущений фактический режим отличается от заданного. В нормально функционирующей системе фактический режим отличается от заданного незначительно, отклонения переменных от требуемых значений малы. Это обстоятельство и позволяет произвести линеаризацию на основе разложения нелинейных функций в ряд Тейлора.

Линеаризация может быть проведена по отдельным звеньям. Произведем в общем виде линеаризацию уравнения (4), считая заданный режим в системе режимом стабилизации.

Отклонения воздействи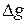й и 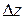от постоянных значений g ₀ и z ₀ вызовут в соответствии с (4) отклонение 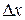выходной координаты x:

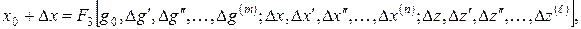(7)

Раскладывая правую часть (7) в ряд Тейлора в окрестности точек x ₀, g ₀, z ₀ и удерживая в разложении только отклонения первой степени, получим

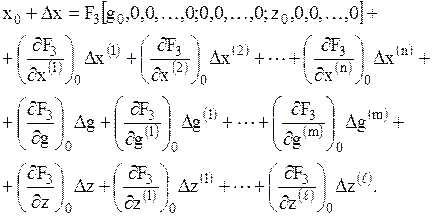
(8)

Вычитая из (8) почленно уравнение статики (6), находим:

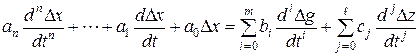(9)

где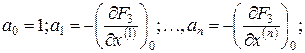

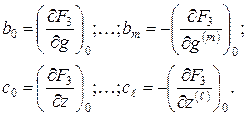
Уравнение (9) является линейным дифференциальным уравнением с постоянными коэффициентами и называется уравнением первого приближения.

Уравнения первого приближения играют чрезвычайно большую роль в исследовании систем автоматического управления весьма широкого класса.

Эти уравнения положены A.M. Ляпуновым в основу создания теории устойчивости движения систем.

Геометрическая трактовка изложенного выше способа линеаризации заключается в следующем. Изобразим статическую характеристику системы x ₀= F (g ₀) при некотором значении z = z ₀ (рис.3).

Рисунок 3

Отметим на ней точку, соответствующую рабочемурежиму, и проведем в этой точке касательную. Тогда

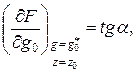
где 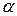- угол наклона касательной к статической характеристике в точке .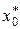

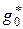Отсюда наглядно видно, что малое приращение выходной переменной вызывает линейное изменение выходной координаты

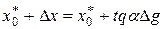
а для приращенийимеем уравнение

.

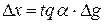Аналогичные геометрические представления справедливы и относительно других переменных правой части уравнения(4).

Таким образом, проведенная аналитически линеаризация соответствует замене нелинейной кривой, связывающей входные и выходные величины, а также их производные прямой линией, и переносу начала координат в точку, соответствующую рабочему режиму.

Аналогичным образом могут быть получены уравнения первого приближения для случая, когда заданный режим в системе не является режимом стабилизации.

Вопрос 3. Пример линеаризации дифференциального уравнения САУ.

Рассмотрим в качестве примера процесс составления и линеаризации дифференциального уравнения системы ФАПЧ, функциональная схема которой приведена на рис.3.1.

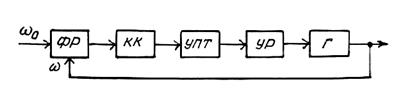
Рисунок 3.1

Запишем уравнения отдельных элементов системы.

Фазовый различитель (фазовый детектор). На него поступают колебанияэталонного и стабилизируемого генераторов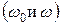

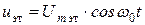, (3.1)

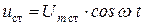. (3.2)

Будем полагать, что среднее значение выходного напряжения фазового различителя меняется по косинусоидальному закону в зависимости от сдвига фаз между колебаниями:

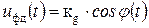. (3.3)

Данный элемент является нелинейным.

Линеаризацию произведем в окрестности точки устойчивого равновесия в системе.

Угол 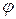, соответствующий данной точке, обозначим через .

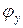Разложим косинусоидальную функцию в ряд около точки 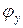и ограничимся двумя членами:

,

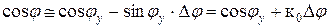где обозначено - .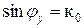

Тогда уравнение (3.3) можно заменить линейным

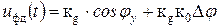. (3.4)

Корректирующий контур обычно выполняется на RС - элементах и может иметь вид (рис.3.1).

Найдем уравнение, связывающее выходное напряжение корректирующего контура с входным.

Для этого воспользуемся вторым законом Кирхгофа и запишем равенство, считая контур работающим на холостом ходу:

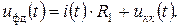(3.5)

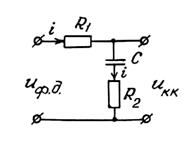
Рисунок 3.2

Из (3.5) имеем

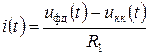(3.6)

Поскольку

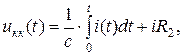
то

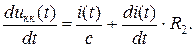(3.7)

Подставляя (3.6) в (3.7), находим

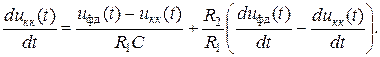
После несложных преобразований получаем

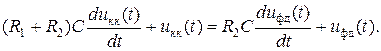(3.8)

Как видноиз (3.8), корректирующий контур, схема которого изображена на рис. 3.2, описывается линейным дифференциальным уравнением первого порядка.