
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Частотні критерії стійкості
|
|
Для оцінки стійкості системи, замкнутої при відомій її АФЧХ, використовують частотний критерій Найквіста – Михайлова. Необхідна АФЧХ розімкнутої системи може бути отримана наступним чином.
Якщо є передавальна функція розімкнутої системи 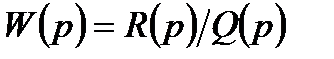 , де
, де 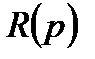 і
і 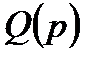 – поліноми від p, то, замінивши р на jw, отримаємо рівняння АФЧХ розімкнутої системи
– поліноми від p, то, замінивши р на jw, отримаємо рівняння АФЧХ розімкнутої системи 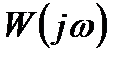 . Щоби побудувати АФЧХ, необхідно представити її такою, що складається з дійсної і уявної частин:
. Щоби побудувати АФЧХ, необхідно представити її такою, що складається з дійсної і уявної частин: 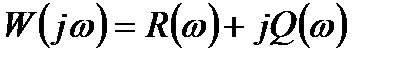 .
.
Потім, задаючись значеннями w від 0 до ¥: 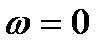 ;
; 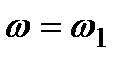 ;
;  і т.д., необхідно знайти точки
і т.д., необхідно знайти точки 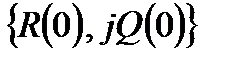 ,
, 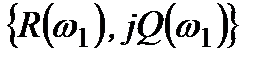 ,
, 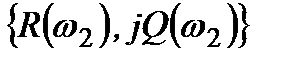 ,... і побудувати АФЧХ на комплексній площині (рис. 4.2, а).
,... і побудувати АФЧХ на комплексній площині (рис. 4.2, а).
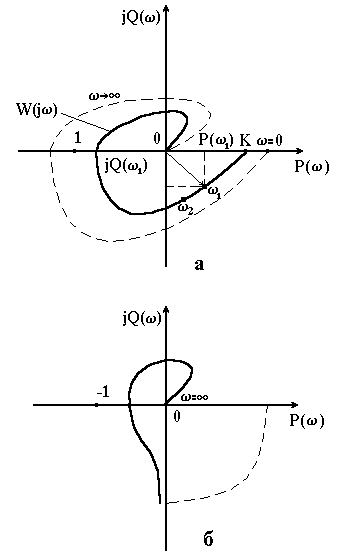 Рисунок 4.2 – АФЧХ стійкої (а) і що знаходиться на межі стійкості (б) розімкнутих систем, які будуть стійкими в замкнутому стані
Рисунок 4.2 – АФЧХ стійкої (а) і що знаходиться на межі стійкості (б) розімкнутих систем, які будуть стійкими в замкнутому стані
|
Розглянемо основні властивості АФЧХ розімкненої системи. Якщо розімкнена система не має інтегруючих ланок, то при 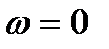 її АФЧХ починається на дійсній осі в точці
її АФЧХ починається на дійсній осі в точці 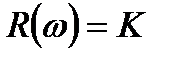 , де К – коефіцієнт підсилення розімкнутої системи. Закінчується АФЧХ при
, де К – коефіцієнт підсилення розімкнутої системи. Закінчується АФЧХ при 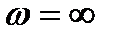 на початку координат (рис. 4.2, б).
на початку координат (рис. 4.2, б).
Важливо відзначити, що розімкнена система може бути стійкою, нестійкою або знаходитись на межі стійкості. Якщо система складається тільки зі стійких елементів, то вона буде стійкою в розімкнутому стані. За наявності хоча б одного нестійкого елемента вона буде нестійкою. За наявності однієї інтегруючої ланки розімкнута система знаходиться на межі стійкості (в літературі такі системи інколи називають нейтрально-стійкими).
Сформулюємо тепер критерій Найквіста-Михайлова (частковим критерій стійкості називають завдяки тому, що він був розроблений Найквістом для дослідження підсилювачів із зворотним зв’язком, а Михайлов узагальнив цей критерій для дослідження стійкості замкнутих автоматичних систем):
якщо розімкнута система стійка або знаходиться на межі стійкості, то для того, щоб замкнута система була стійка, необхідно і достатньо, щоби амплітудно-фазова частотна характеристика розімкненої системи при зміні w від 0 до ¥ не охоплювала точку з координатами {–1, j0}. Якщо розімкнена система нестійка, а її передавальна функція має m полюсів справа від уявної осі площини р, то для стійкості замкнутої системи необхідно і достатньо, щоби АФЧХ розімкнутої системи при зміні w від -¥ до +¥ охоплювала точку {–1, j0} m разів.
Як визначити, чи охоплює АФЧХ розімкнутої системи точку  , якщо розімкнута система знаходиться на межі стійкості, бо АФЧХ при
, якщо розімкнута система знаходиться на межі стійкості, бо АФЧХ при 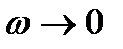 прямує до нескінченності. В цьому випадку уявно з’єднують кінець АФЧХ при
прямує до нескінченності. В цьому випадку уявно з’єднують кінець АФЧХ при 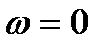 з додатною дійсною піввіссю другого кола, нескінченно великого радіуса (рис. 4.2, б). Тоді можна однозначно визначити, чи охоплює АФЧХ точку
з додатною дійсною піввіссю другого кола, нескінченно великого радіуса (рис. 4.2, б). Тоді можна однозначно визначити, чи охоплює АФЧХ точку 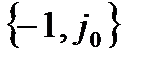 .
.
Чому у випадку стійкості розімкненої системи розглядається АФЧХ при зміні w від 0 до ¥, а у випадку нестійкої – при зміні w від -¥ до +¥? На практиці АФЧХ може бути знята тільки для додатних частот ( ). З математичної точки зору АФЧХ повинні будуватись для всього діапазону частот –
). З математичної точки зору АФЧХ повинні будуватись для всього діапазону частот –  , при цьому гілка АФЧХ для від’ємних частот симетрична відносно дійсної осі гілки, побудованої для додатних частот, якщо ця гілка не охоплює або охоплює точку
, при цьому гілка АФЧХ для від’ємних частот симетрична відносно дійсної осі гілки, побудованої для додатних частот, якщо ця гілка не охоплює або охоплює точку 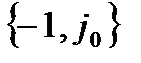 m разів. Якщо ж розглядати тільки додатну ланку (гілку), то вона повинна охоплювати цю точку
m разів. Якщо ж розглядати тільки додатну ланку (гілку), то вона повинна охоплювати цю точку 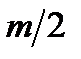 разів. Наприклад, при
разів. Наприклад, при 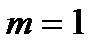 вона повинна охоплювати її ½ разу. Але таке визначення доволі невдале. Тому при нестійкій розімкненій системі розглядають дві гілки її АФЧХ, тобто беруть діапазон зміни частоти від -¥ до +¥ (рис. 4.3). Звідси видно, що при використанні частотного критерію стійкості визначним є положення АФЧХ розімкненої системи поблизу точки
вона повинна охоплювати її ½ разу. Але таке визначення доволі невдале. Тому при нестійкій розімкненій системі розглядають дві гілки її АФЧХ, тобто беруть діапазон зміни частоти від -¥ до +¥ (рис. 4.3). Звідси видно, що при використанні частотного критерію стійкості визначним є положення АФЧХ розімкненої системи поблизу точки 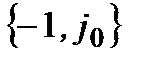 .
.
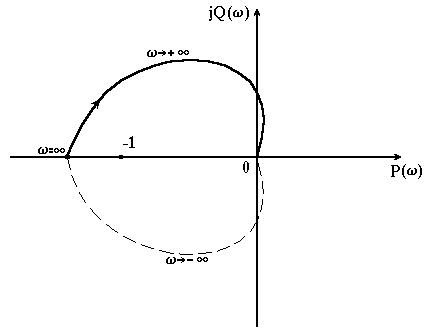 Рисунок 4.3 – АФЧХ нестійкої розімкнутої системи (m=1), яка буде стійкою
в замкнутому стані
Рисунок 4.3 – АФЧХ нестійкої розімкнутої системи (m=1), яка буде стійкою
в замкнутому стані
|
За допомогою критерію Найквіста-Михайлова, як і критерію стійкості Михайлова, можна оцінити вплив параметрів елементів системи на її стійкість. Для цього необхідно побудувати АФЧХ розімкнутої системи при даному значенні параметра і визначити стійкість замкнутої системи. Нехай для прикладу система є стійкою (рис. 4.4). Змінимо значення цього параметра. Нехай при новому значенні параметра (наприклад, при більшому) АФЧХ набула вигляду, зображеного на рис. 4.4 пунктиром. Отже, збільшення параметра спонукає нестійкості системи.
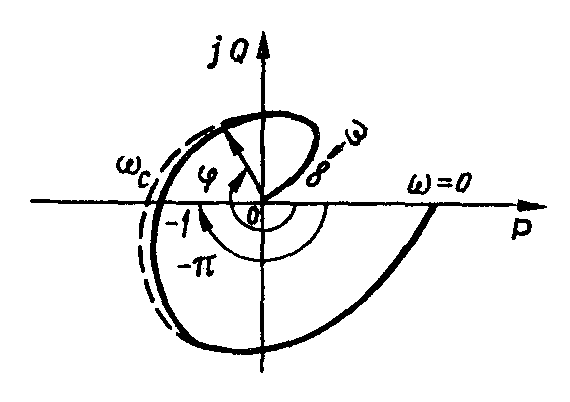 Рисунок 4.4 – АФЧХ стійкої розімкнутої системи
Рисунок 4.4 – АФЧХ стійкої розімкнутої системи
|
Так як критерій Найквіста-Михайлова використовує експериментально зняті АФЧХ, то неважко дати його фізичну трактовку. Пояснимо це спочатку на прикладі системи, яка знаходиться на межі стійкості. В цьому випадку АФЧХ розімкненої системи при деякій частоті 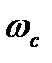 проходить через точку
проходить через точку 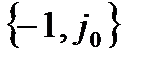 (рис. 4.4). Це означає, що при даній частоті
(рис. 4.4). Це означає, що при даній частоті 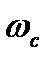 амплітуда вихідного сигналу дорівнює амплітуді вхідного сигналу, а його фаза прямо протилежна фазі вхідного сигналу, тобто зсув по фазі між ними дорівнює -p. При замиканні системи основний зворотний зв’язок повинен бути від’ємний, тобто фазу вихідного сигналу при подачі його на вхід системи слід повернути на p. Крім того, при цьому слід відключити зовнішнє джерело коливань, яке подавало гармонійні сигнали на вхід системи.
амплітуда вихідного сигналу дорівнює амплітуді вхідного сигналу, а його фаза прямо протилежна фазі вхідного сигналу, тобто зсув по фазі між ними дорівнює -p. При замиканні системи основний зворотний зв’язок повинен бути від’ємний, тобто фазу вихідного сигналу при подачі його на вхід системи слід повернути на p. Крім того, при цьому слід відключити зовнішнє джерело коливань, яке подавало гармонійні сигнали на вхід системи.
Отже, при замиканні системи вихідний сигнал (правда, тепер він вже не буде вихідним, оскільки він поданий на вхід системи, але ми знову для якості будемо його називати вихідним) буде співпадати за амплітудою і фазою з вхідним сигналом, тобто при замиканні системи в ній нічого не зміниться. В системі встановляться незатухаючі коливання, причому вони будуть підтримуватись не за рахунок енергії джерела вхідного сигналу (воно тепер відключене), а за рахунок енергії самої системи. Це і означає знаходження системи на межі стійкості.
Якщо АФЧХ при частоті 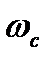 перетинає дійсну вісь зліва від точки
перетинає дійсну вісь зліва від точки 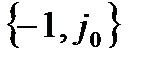 , то вона охоплює дану точку. Це свідчить про те, що в розімкнутій системі амплітуда вихідного сигналу на даній частоті
, то вона охоплює дану точку. Це свідчить про те, що в розімкнутій системі амплітуда вихідного сигналу на даній частоті 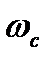 більша від амплітуди вхідного сигналу, а зсув по фазі між ними дорівнює -p. При замиканні системи і відключенні джерела зовнішніх коливань амплітуда вихідних коливань буде зростати, тобто система буде нестійкою. Якщо АФЧХ не охоплює точки
більша від амплітуди вхідного сигналу, а зсув по фазі між ними дорівнює -p. При замиканні системи і відключенні джерела зовнішніх коливань амплітуда вихідних коливань буде зростати, тобто система буде нестійкою. Якщо АФЧХ не охоплює точки 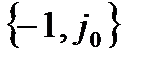 , то при зсуві по фазі, рівному -p, амплітуда вихідного сигналу менша, ніж амплітуда вхідного сигналу. В цьому випадку при замиканні системи коливання в ній будуть затухати, тобто система буде стійкою.
, то при зсуві по фазі, рівному -p, амплітуда вихідного сигналу менша, ніж амплітуда вхідного сигналу. В цьому випадку при замиканні системи коливання в ній будуть затухати, тобто система буде стійкою.
Тепер розглянемо, як використати частотний критерій стійкості Найквіста-Михайлова, якщо в розпорядженні є не АФЧХ, а ЛАЧХ розімкненої системи. Сформулюємо даний критерій для даного випадку.
Замкнута мінімально фазова система стійка, якщо при досягненні фазової частотною характеристикою значення -p логарифмічна амплітудно-частотна характеристика буде від’ємною (рис. 4.5). До мінімально-фазових систем відносяться такі, порядок числівника передавальної функції 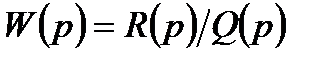 яких нижчий порядку знаменника і відсутні нулі передавальної функції (корені рівняння
яких нижчий порядку знаменника і відсутні нулі передавальної функції (корені рівняння 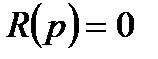 ) в правій півплощині р.
) в правій півплощині р.
Чому розглядається ЛАЧХ при значенні фази, рівному
-p? Тому що стійкість згідно з критерієм Найквіста-Михайлова оцінюється тим, з якого боку від точки 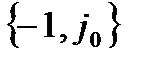 АФЧХ перетинає дійсну вісь комплексної площини, а при перетині дійсної осі фаза АФЧХ дорівнює -p.
АФЧХ перетинає дійсну вісь комплексної площини, а при перетині дійсної осі фаза АФЧХ дорівнює -p.
Якщо ЛАЧХ від’ємна, то модуль АФЧХ менший одиниці, оскільки числа, менші одиниці, мають від’ємні логарифми. Від’ємність ЛАЧХ при фазі -p свідчить про те, що АФЧХ розімкнутої системи не охоплює точку 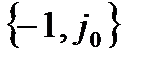 .
.
Чому при оцінці стійкості системи за ЛАЧХ вважається, що критерій Найквіста-Михайлова можна використовувати тільки для мінімально-фазових систем, адже при використанні АФЧХ такого обмеження не було? Це пояснюється тим, що при оцінці стійкості за ЛАЧХ розглядається тільки частина її при фазі, близькій до -p, або частина АФЧХ в околі перетину нею дійсної осі. Тільки для мінімально-фазових систем розгляд частини АФЧХ (ЛАЧХ) свідчить про всю характеристику. Для немінімально-фазових систем це зробити неможливо.
Всі розглянуті критерії стійкості тим або іншим способом оцінюють один і той же факт: чи є серед коренів характеристичного рівняння замкнутої системи корені з додатною дійсною частиною. Тому всі вони дають однаковий результат в оцінці стійкості системи.
Відзначимо, що у всіх випадках перш ніж досліджувати стійкість за допомогою того чи іншого критерію, слід впевнитись, що необхідна умова стійкості виконується, тобто всі коефіцієнти характеристичного рівняння системи є додатними числами.
|
|