
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Побудова довірчих інтервалів
|
|
Надійність оцінки визначається ймовірністю, з якою стверджується що побудований за результатами вибірки довірчий інтервал містить невідомий параметр генеральної сукупності. Ймовірність інтервальної оцінки параметра називають довірчою і позначають p. Тоді можна сподіватися, що при множині спостережень параметр генеральної сукупності буде правильно оцінений (тобто довірчий інтервал покриє дійсне значення цього параметра) приблизно у p × 100% випадків і лише у (100– p) % випадків оцінка буде помилковою.
Ризик помилки визначається рівнем значущості a, який називається довірчим рівнем даного інтервалу.
Позначимо параметр генеральної сукупності через λ, а його оцінку – μ. Тоді, за означенням довірчого інтервалу, будемо мати наступну формулу:
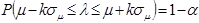 ,
,
де k – довірчий множник, який відображає частку стандартного відхилення, яка повинна бути врахована, щоб із заданою ймовірністю p довірчий інтервал 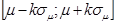 покрив параметр λ генеральної сукупності.
покрив параметр λ генеральної сукупності.
Перейдемо до побудови довірчих інтервалів для параметрів парної лінійної регресії. Знайдемо довірчий інтервал для оціночного рівняння. Для цього нам необхідно мати похибку оцінки, яку знайдемо за формулою: 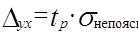 , де tp – ймовірнісний коефіцієнт, значення якого при заданому рівні ймовірності p знаходимо за таблицями нормального розподілу. Значення tp є коренем рівняння 2Ф(tp) = p, де Ф(tp) – інтегральна функція Лапласа.
, де tp – ймовірнісний коефіцієнт, значення якого при заданому рівні ймовірності p знаходимо за таблицями нормального розподілу. Значення tp є коренем рівняння 2Ф(tp) = p, де Ф(tp) – інтегральна функція Лапласа.
Тоді довірчий інтервал для оціночного рівняння матиме вигляд:
 . (1.20)
. (1.20)
Графічно довірчий інтервал можна зобразити таким чином: 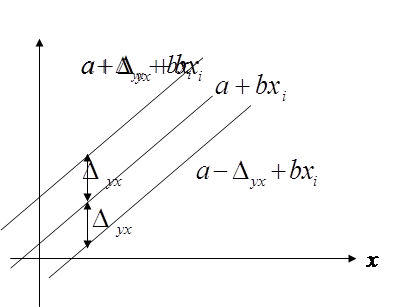
Рис. 1.7. Довірчий інтервал оціночного рівняння
Процедура побудови довірчих інтервалів для параметрів a та b аналогічна попередній процедурі. Спочатку знаходимо граничні похибки оцінок відповідних параметрів за формулами:
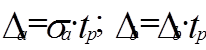 (1.21)
(1.21)
де  – відповідно дисперсії оцінок a та b, значення яких обчислюються за формулами:
– відповідно дисперсії оцінок a та b, значення яких обчислюються за формулами:
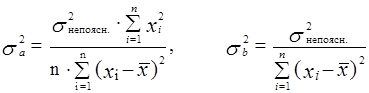 (1.22)
(1.22)
Отже, довірчі інтервал для параметрів a та b матимуть вигляд:
 , (1.23)
, (1.23)
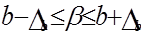 . (1.24)
. (1.24)
Приклад 1.3. На основі даних прикладів 1.1 та 1.2 побудувати довірчі інтервали оціночного рівняння і параметрів a та b економетричної моделі для ймовірності p =0, 9.
¨ Розв’язування.
Обчислимо граничну похибку  . Значення tp знайдемо, розв’язавши рівняння:
. Значення tp знайдемо, розв’язавши рівняння: 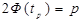 , де Ф(tp) - інтегральна функція Лапласа. Для р =0, 9 маємо: tр =1, 65. Також знайдемо
, де Ф(tp) - інтегральна функція Лапласа. Для р =0, 9 маємо: tр =1, 65. Також знайдемо 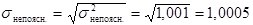
Тоді  .
.
Довірчий інтервал матиме вигляд:
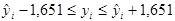 ,
,
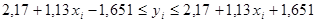 ,
,
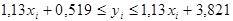 .
.
Для побудови оціночного рівняння, верхньої та нижньої межі довірчого інтервалу достатньо по дві точки. Обчислимо їх:
Нижня межа

| Оціночна пряма
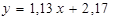
| Верхня межа
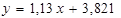
| |||
| x | y | x | y | x | y |
| 1, 65 | 3, 30 | 4, 95 | |||
| 11, 82 | 13, 47 | 15, 12 |
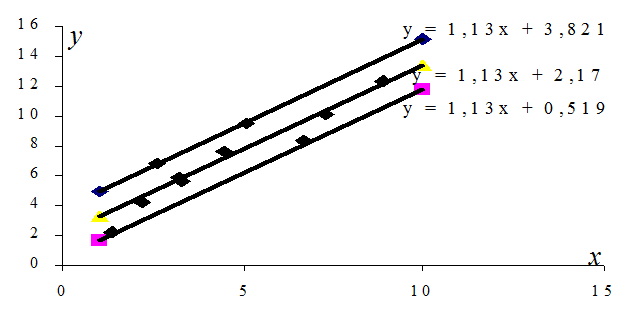 |
Знайдемо довірчі інтервали для a та b. Почнемо із обчислення граничних похибок оцінок цих параметрів:
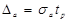 ,
, 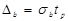 .
.
Для цього спочатку знайдемо значення дисперсій і середніх квадратичних відхилень оцінок а та b за формулами:
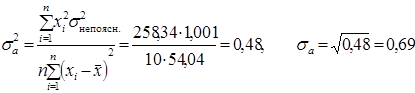 .
.
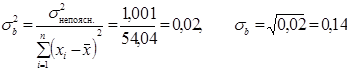 .
.
Далі знайдемо
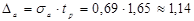 ;
;
 .
.
Отже, нами отримано наступні інтервали довіри для оцінки a:
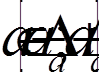 ,
,
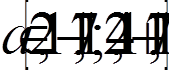 ,
,
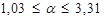 ,
,
для оцінки b:
 ,
,
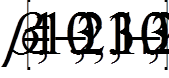
 .
.
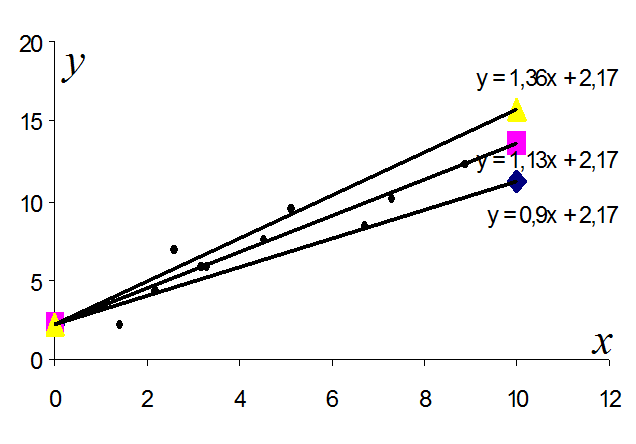
Відобразимо ці довірчі інтервали графічно. Обчислимо координати двох точок для побудови нижньої та верхньої меж довірчого інтервалу для a.
Нижня межа
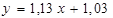
| Оціночна пряма
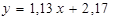
| Верхня межа

| |||
| x | y | x | y | x | y |
| 2, 16 | 3, 30 | 4, 44 | |||
| 12, 33 | 13, 47 | 14, 61 |
 |
Для b:
Нижня межа
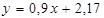
| Оціночна пряма
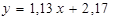
| Верхня межа
| |||
| x | y | x | y | x | y |
| 2, 17 | 2, 17 | 2, 17 | |||
| 11, 17 | 13, 47 | 15, 77 |
 |
9. Перевірка нульових гіпотез
Оскільки статистичні дані, які ми досліджуємо, створені різними випадковими факторами, то більшість статистичних досліджень супроводжується перевіркою деяких припущень або гіпотез про джерела цих даних.
Основне припущення, яке перевіряється, називається нульовою гіпотезою і позначається Но переважно формулюється як відсутність різниць, відсутність впливу фактора, рівність нулю значень вибіркових характеристик і т.д.
Друге припущення, яке перевіряється (не завжди строго протилежне чи обернене першому), називається конкуруючою або альтернативною гіпотезою і позначається Н1.
Для статистичного висновку про наявність або відсутність кореляційного зв’язку між досліджуваними змінними необхідно провести перевірку рівня значущості вибіркового коефіцієнта кореляції. Використаний критерій для розв’язку задач даного типу ґрунтується на розподілі різних статистик і називається критерієм значущості.
Процедура перевірки значущості починається з формулювання нульової гіпотези Но. У загальному випадку вона полягає в тому, що між параметром вибірки і параметром генеральної сукупності немає ніяких суттєвих різниць. Альтернативна гіпотеза Н1 полягає в тому, що між цими параметрами є суттєві різниці. Наприклад, при перевірці наявності кореляції в генеральній сукупності нульова гіпотеза полягає в тому, що істинний коефіцієнт кореляції рівний нулю (Но: R =0). Якщо в результаті перевірки виявиться, що нульова гіпотеза неприйнятна, то нульова гіпотеза відкидається і приймається альтернативна Н1. Іншими словами, припущення відносно некорельованості випадкових змінних у генеральній сукупності треба визнати необґрунтованим. І навпаки, якщо на основі критерію значущості нульова гіпотеза приймається, тобто r міститься в допустимій зоні випадкового розсіяння, тоді немає підстави вважати сумнівним припущення відносно некорельованості змінних у генеральній сукупності.
При перевірці значущості встановлюють значення її рівня a, який дає певну впевненість в тому, що помилкові висновки будуть зроблені в дуже рідких випадках. Рівень значущості виражає ймовірність того, що нульова гіпотеза Но відкидається тоді, коли вона в дійсності вірна. Зрозуміло, що має сенс вибрати дану ймовірність як можна меншою.
Перевіряючи значущість коефіцієнта парної кореляції, встановлюють наявність або відсутність кореляційного зв’язку між досліджуваними явищами. При відсутності зв’язку коефіцієнт кореляції генеральної сукупності рівний нулю (R =0). Процедура перевірки гіпотези починається з формулювання нульової та альтернативної гіпотез:
Н о: різниці між вибірковим коефіцієнтом кореляції r та R =0 немає;
Н 1: різниця між r та R =0 значна, і як наслідок, між змінними у та х в генеральній сукупності є суттєвий лінійний зв’язок.
Для оцінки значущості коефіцієнта кореляції використовуємо t- критерій Стьюдента з n-m-1 ступенями вільності.
Під кількістю ступенів вільності розуміють різницю між кількістю спостережень та кількістю параметрів, які встановлені у результаті цих спостережень, незалежно один від одного.
За результатами вибірки обчислюємо t -статистику, або емпіричне значення параметру t:
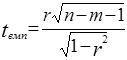 , (1.25)
, (1.25)
яке порівнюється з критичним значенням tкр, що знаходиться за таблицями розподілу Стьюдента при заданому рівні значущості a та k = n - m -1 ступенях вільності.
Правило використання критерію полягає у наступному:
- якщо 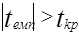 , то нульова гіпотеза Но на рівні значущості α відкидається і приймається альтернативна гіпотеза Н1 про існування лінійної залежності між даними змінними в генеральній сукупності;
, то нульова гіпотеза Но на рівні значущості α відкидається і приймається альтернативна гіпотеза Н1 про існування лінійної залежності між даними змінними в генеральній сукупності;
- якщо  , то нульова гіпотеза Но на рівні значущості α приймається.
, то нульова гіпотеза Но на рівні значущості α приймається.
Перевірку нульових гіпотез стосовно параметрів a та b економетричної моделі проводять аналогічно. Спочатку висуваємо нульові гіпотези:
H0: a =0, H0: b =0.
Альтернативними будуть гіпотези:
H1: a 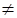 0, H1: b
0, H1: b 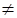 0.
0.
Потім обчислюємо емпіричні значення параметра t за формулами:
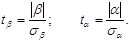
Емпіричне значення параметру порівнюють з критичним, знайденим за таблицями Стьюдента для заданого рівня значущості a та k = n - m -1 ступенів вільності. Якщо 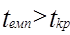 , то нульова гіпотеза Но із рівнем значущості α відкидається і приймається альтернативна гіпотеза Н1. Тоді відповідна оцінка вважається статистично значимою. Якщо ж
, то нульова гіпотеза Но із рівнем значущості α відкидається і приймається альтернативна гіпотеза Н1. Тоді відповідна оцінка вважається статистично значимою. Якщо ж 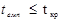 , то нульова гіпотеза Но для рівня значущості α приймається, а відповідна оцінка не є статистично значимою.
, то нульова гіпотеза Но для рівня значущості α приймається, а відповідна оцінка не є статистично значимою.
Приклад 1.4. На основі даних прикладів 1.1-1.3 виконати перевірки нульових гіпотез стосовно коефіцієнта кореляції і параметрів a та b економетричної моделі.
¨ Розв’язування.
Висуваємо нульову гіпотезу Но: Rген =0 (робимо припущення, що коефіцієнт кореляції генеральної сукупності рівний нулю). Альтернативною гіпотезою буде Н1: Rген ¹ 0.
Далі для заданої вибірки обчислимо емпіричне значення параметру t:

Для заданої ймовірності р =0, 9 (a =1- р=1-0, 9=0, 1) і k=10-1-1=8 ступенів вільності знаходимо табличне значення tкр.=2, 306.
Оскільки  , то з надійністю р =0, 9 гіпотезу Но необхідно відкинути і прийняти альтернативну гіпотезу Н1 про існування залежності між змінними. Отже, у 90 % вибірок із генеральної сукупності коефіцієнт кореляції не дорівнює нулю.
, то з надійністю р =0, 9 гіпотезу Но необхідно відкинути і прийняти альтернативну гіпотезу Н1 про існування залежності між змінними. Отже, у 90 % вибірок із генеральної сукупності коефіцієнт кореляції не дорівнює нулю.
Далі виконаємо перевірку нульової гіпотези відносно β (Но: β =0) проти альтернативної Н1: β ¹ 0. Для цього знаходимо емпіричне значення за формулою:
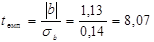
Оскільки емпіричне значення t більше критичного (tемп> tкр), то нульова гіпотеза відхиляється і робиться висновок, що кутовий коефіцієнт b розрахований за даною вибіркою є статистично значущим з ймовірністю р =0, 9.
Перевіримо нульову гіпотезу Но: α =0. Обчислимо
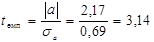 .
.
tемп> tкр, значить нульова гіпотеза стосовно параметру α теж відхиляється, а значить α не може бути рівним нулю в генеральній сукупності.
|
|