Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Для новых пользователей первый месяц бесплатно. Чат-бот для мастеров и специалистов, который упрощает ведение записей: — Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать; Начать пользоваться сервисом
Решение аналитическим способом
|
|
Межрегиональный центр переподготовки специалистов
Контрольная работа
по дисциплине: теория массового обслуживания
Выполнила: Ирина Свистуненко
Группа: ПБТ-49
Вариант: 1
Проверила: Разинкина Т.Э.
Новосибирск
2015.
Постановка задачи
Промежуточное звено компьютерной сети Supernet обслуживает запросы от 5 абонентов по двум телефонным каналам. Компьютер каждого абонента выходит на связь по любому свободному каналу. Если же оба канала заняты, абонент получает отказ. Администрация решила провести статистическое исследование для того, чтобы оценить целесообразность реконструкции сети (таблица 1 задания). Специальная программа фиксировала продолжительность работы каждого компьютера (таблица 3 задания) и число обращений в сутки (таблица 2 задания).
Необходимо оценить вероятность отказа при подключении к сети после реконструкции двумя способами:
1) аналитически, при этом считать интенсивность работы каждого терминала одинаковой (то есть усреднённой);
2) методом Монте-Карло, при этом использовать не усреднённые оценки интенсивностей. По результатам работы программы построить доверительный интервал для вероятности отказа при уровне значимости 0.05.
Вариант контрольной работы определяется по последней цифре пароля. Согласно варианту определяются:
- планируемые изменения в сети (таблица 1 задания);
- количество подключений каждого абонента (таблица 2 задания);
- время работы каждого абонента (таблица 3 задания).
Контрольная работа должна содержать:
- постановку задачи (вместе с данными из таблиц 2 и 3 задания);
- полное решение аналитическим способом (граф системы, формулы, вычисленные значения и комментарии вычислений);
- программу на языке С или Pascal, моделирующую работу системы методом Монте–Карло любым из двух способов, описанных в п.2.2 (эта же программа может вычислять интенсивности по таблицам 2 и 3); наличие комментариев в программе обязательно;
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
- результаты работы программы;
- построение доверительного интервала по результатам работы программы.
Для варианта 1:
планируемые изменения (из таблицы 1 задания): добавить ещё один канал;
Таблица 1 (таблица 2 задания). Количество подключений в сутки
| 1 компьютер | ||||||||||||
| 2 компьютер | ||||||||||||
| 3 компьютер | ||||||||||||
| 4 компьютер | ||||||||||||
| 5 компьютер |
Таблица 2 (таблица 3 задания). Время работы в часах
| 1 компьютер | 0.50 | 0.56 | 0.51 | 0.40 | 1.41 | 0.23 | 0.48 | 0.28 | 0.23 | 1.48 |
| 2 компьютер | 0.45 | 0.05 | 1.26 | 1.08 | 1.07 | 1.29 | 1.23 | 0.77 | 1.13 | 3.30 |
| 3 компьютер | 0.25 | 1.42 | 3.21 | 0.78 | 0.26 | 1.12 | 2.21 | 0.02 | 0.06 | 1.36 |
| 4 компьютер | 0.64 | 0.43 | 0.40 | 0.59 | 1.65 | 2.20 | 0.34 | 2.34 | 1.22 | 0.36 |
| 5 компьютер | 1.49 | 3.85 | 0.70 | 0.14 | 0.79 | 0.38 | 0.35 | 3.24 | 0.38 | 0.17 |
Решение аналитическим способом
Это случай системы массового обслуживания с отказами и ограниченным числом требований в системе. “Приборами” в данном случае являются каналы, по которым происходит подключение к сети.
Введём следующие состояния системы: 0 – все каналы свободны, 1 – один канал занят (другой при этом свободен), 2 – заняты оба канала.
Обозначим как l – средняя интенсивность подключения для одного компьютера, а m – средняя интенсивность освобождения канала для одного компьютера.
Граф системы для случая двух каналов изображён на рис. 1.
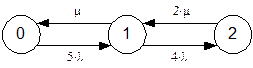
Рис. 1. Система из 5-ти компьютеров и 2-ух каналов (Система_1)
Найдём l и m по статистическим данным. У нас имеется два потока событий: с одной стороны, поток заявок на подключение к сети от компьютеров, с другой стороны – поток “освобождения каналов”. Число наступления события за время t – случайная величина, подчиняющаяся распределению Пуассона с параметром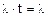 
за единицу времени. Методом максимального правдоподобия была получена оценка для параметра этого распределения: 
.
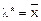Обозначим данные из таблицы 1 через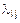 
, где i – номер строки, j – номер столбца. Найдем оценки интенсивности “подключения к каналам” для каждого компьютера по формуле: 
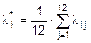. Тогда:
;
;
;
;
.
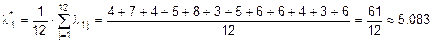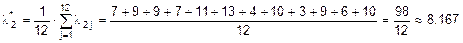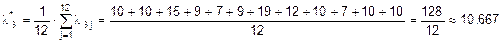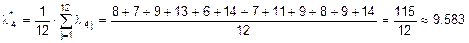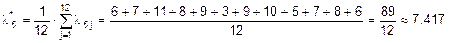Усредняем полученные значения:
.
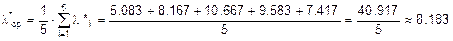Время между наступлениями соседних событий в простейшем потоке – экспоненциально-распределенная случайная величина, и оценкой параметра такого распределения будет: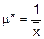 
.
Обозначим данные из таблицы 2 через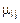 
, где i – номер строки, j – номер столбца. Найдем оценки “ интенсивности освобождения” для каждого канала по формуле: 
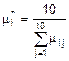. Так как данные в таблицах 1 и 2 даны в разных единицах измерения, в сутках и часах, соответственно, то необходимо выбрать общую единицу измерения. В качестве общей единицы измерения выбираем сутки. Тогда переводим интенсивности освобождения каналов в сутки и получаем:
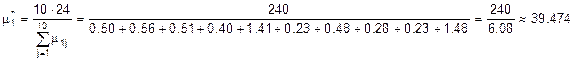сут–1;
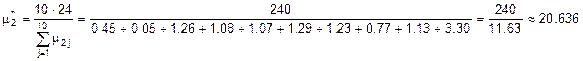сут–1;
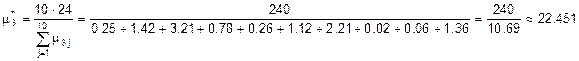сут–1;
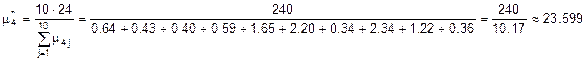сут–1;
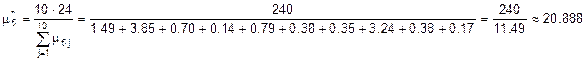сут–1.
Усредняем полученные значения:
.
Если система из 5-ти компьютеров и двух каналов (Система_1), см. рис. 1, находится в состоянии 2 (оба канала заняты), то попытка подключиться к сети ещё с одного компьютера обречена на неудачу. Следовательно, вероятность нахождения Системы_1 в состоянии 2 и будет вероятностью отказа.
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
Так как Система_1 имеет конечное число состояний, то предельные вероятности всегда существуют и могут быть найдены следующим образом:
;
;
.
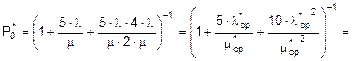
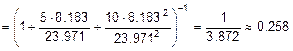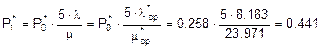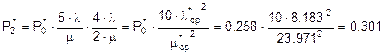Таким образом, вероятность отказа при двух каналах равна 0.301.
После планируемой реконструкции сети к Системе_1 будет добавлен ещё один канал. Для полученной системы из 5-ти компьютеров и трёх каналов (Система_2) составим граф состояний, приведённый на рис. 2. Для реконструированной системы возможны следующие состояния: 0 – все каналы свободны, 1 – один канал занят (два других при этом свободны), 2 – заняты два канала (один при этом свободен), 3 – заняты все три канала.
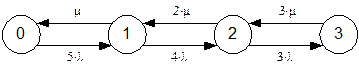
Рис. 2. Система из 5-ти компьютеров и 3-ёх каналов (Система_2)
Если Система_2 находится в состоянии 3 (все три канала заняты), то попытка подключиться к сети ещё с одного компьютера обречена на неудачу. Следовательно, вероятность нахождения Системы_2 в состоянии 3 и будет искомой вероятностью отказа.
Так как Система_2 имеет конечное число состояний, то предельные вероятности всегда существуют и могут быть найдены следующим образом:
;
;
;
.
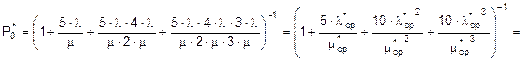
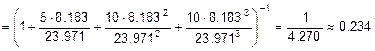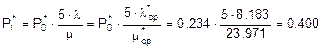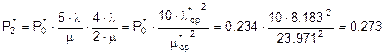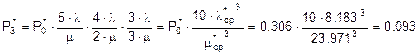Таким образом, вероятность отказа при трёх каналах равна 0.093.
Ответ: после добавления третьего канала вероятность отказа снизится с 0.301 до 0.093, то есть в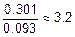 
раза.
|
|