Фур’є-перетворення в когерентно-оптичній системі

Лабораторна робота № 2

Основною елементарною операцією в когерентній оптиці є двовимірне фур'є-перетворення, яке виконується простою сферичною лінзою над двовимірним когерентним оптичним сигналом. Багато інших математичних операцій можна реалізувати на базі оптичного фур'є-перетворення.

Опишемо процедуру виконання сферичною лінзою оптичного фур'є-перетворення. Для цього розглянемо наведену на рис. 1 оптичну систему, що містить вхiдну площину P₁(x,y), лінза Л і вихідну площину P₂(x,h). У цій схемі віддаль між площиною P₁ і лінзою Л рівна d, а віддаль між лінзою Л і площиною P₂ рівна f, причому f – фокусна віддаль лінзи Л. Нехай у площині P₁ розташований просторовий модулятор світла (ПМС), комплексне амплітудне пропускання якого описується виразом

,

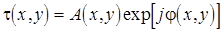де - розподіл амплітудного пропускання, 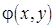- розподіл фази. Модулятор просвічують плоскою монохроматичною лінійно поляризованою хвилею, що поширюється перпендикулярно до P₁ вздовж осі z. Під час проходження цієї хвилі через ПМС у площині P₁ формується когерентний оптичний сигнал, розподіл комплексних амплітуд в якому пропорційний комплексному амплітудному пропусканню .

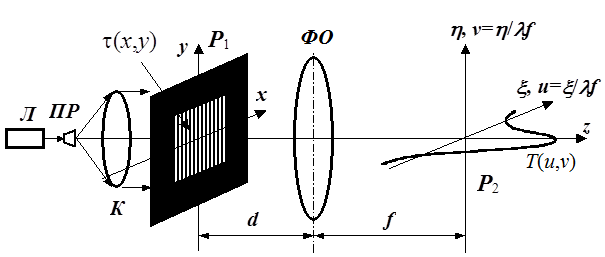
Рис. 1. Схема оптичного фур'є-перетворення: Л – лазер; ПР – пристрій розширення лазерного променя; К – коліматор; u,v – просторові частоти; l - довжина хвилі світла;

На основі принципа Гюйгенса-Френеля, який для дифракції Фраунгофера описується відомою формулою Релея-Зомерфельда, можна показати, що розподіл комплексних амплітуд світла у задній фокальній площині лінзи Л, тобто у площині P₂(x,h), з точністю до квадратичного фазового множника пропорційний двовимірному перетворенню Фур'є від розподілу комплексних амплітуд у площині P₁(x,y). Для координатної площини P₂(u,v), що збігається з площиною P₂(x,h), розподіл комплексних амплітуд описується так:

, (1)

Тут

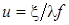, - (2)

просторові частоти, - довжина хвилі випромінювання, 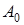- амплітуда плоскої хвилі, що поширюється у додатному напрямі осі z. При цьому вважається, що лінза Л є тонкою, а мінімальні розміри деталей зображення набагато більші за довжину світлової хвилі. Це означає, що лінза затримує фронт падаючої хвилі на значення, пропорційне товщині лінзи у кожній точці, а зміщенням променя всередині лінзи можна знехтувати.

Інтеграл у виразі (1) є двовимірним перетворенням Фур’є функції за умови, що ця функція тотожньо рівна нулю за межами поверхні лінзи. Ця умова дозволяє розширити межі інтегрування до безмежності, що і вимагається для перетворення Фур’є.

У тих випадках, коли інформаційним параметром є лише інтенсивність світла, квадратичний фазовий множник у виразі (1) не враховують. Ефект, зумовлений цим множником, еквівалентний дії тонкої розсію вальної лінзи з фокусною віддалю f, розташованої у площині P₂. Якщо в цю площину помістити тонку збиральну лінзу з фокусною віддалю f, то цей фазовий множник скомпенсується. В результаті отримують оптичну систему, що виконує точне перетворення Фур’є

. (3)

Під час інженерних розрахунків розподілу 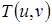множник перед інтегралом можна не враховувати.