
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Метод Зейделя
|
|
Розглянемо метод Зейделя для розв'язування СЛАР, що зведена до нормального вигляду (2.5).
Виберемо вектор початкових наближень
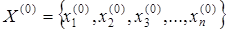
(наприклад, стовпець вільних членів 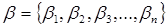 ). Тоді проводимо уточнення значень невідомих чином:
). Тоді проводимо уточнення значень невідомих чином:
1) перше наближення:
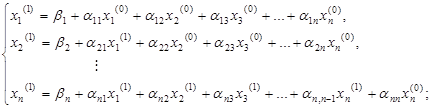
2) k + 1 наближення:
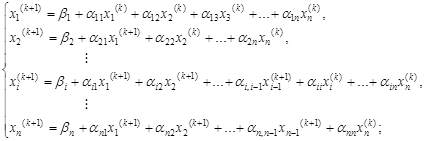
де k = 0, 1, 2, …, n.
Ітераційний процес методу Зейделя подібний до методу простих ітерацій. Відмінним є те, що уточнені значення 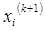 одразу ж підставляються в наступні рівняння. Отже, ітераційна формула методу Зейделя:
одразу ж підставляються в наступні рівняння. Отже, ітераційна формула методу Зейделя:
 .
.
Тобто, метод Зейделя відрізняється від методу простих ітерацій тим, що при обчисленні 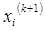 на (k+1)-му кроці враховуються значення
на (k+1)-му кроці враховуються значення 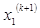 ,
, 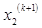 ,
, 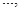
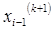 , обчислені на цьому самому кроці.
, обчислені на цьому самому кроці.
З метою економії пам’яті при програмуванні методу Зейделя недоцільно напряму застосовувати подану формулу методу. На відміну від методу простих ітерацій, у методі Зейделя немає необхідності зберігати в пам’яті повністю вектор попередніх наближень розв’язку. Можна застосовувати один вектор, в якому будуть зберігатися останні наближення розв’язків. При цьому для контролю умови завершення ітераційного процесу по кожному з розв’язків можна застосовувати одну й ту ж допоміжну змінну для тимчасового зберігання попереднього наближення чергового розв’язку.
Умова збіжності: метод Зейделя є збіжним, якщо виконується нерівність
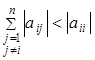 , для всіх i =1, 2,..., n.
, для всіх i =1, 2,..., n.
і якщо хоча б для одного і ця нерівність строга
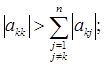
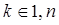 .
.
2.2.6. Розв'язування СЛАР в MATLAB
Програмний пакет MATLAB має потужний пакет для розв'язування СЛАР різними методами.
При реалізації багатьох завдань, пов'язаних з матричної алгеброю, корисними можуть виявитися функції для оцінок основних характеристик:
det(A) – обчислення визначника квадратної матриці;
rank(A) – обчислення рангу матриці A;
inv(A) – обчислення оберненої матриці A-1, та ж сама операція, що й A^(-1);
A^n – піднесення квадратної матриці А до степеня n тощо.
Систему рівнянь типу Ax=b можна розв'язати засобами MATLAB різними методами. Розглянемо деякі з них.
1.Операція зворотної скісної риски \, або функція mldivide. Розв'язок СЛАР виконується командою:
> > x=A\b
або
> > x=mldivide(A, b)
Ці команди є аналогічними. Операція \ реалізується наступним чином.
Якщо матриця A діагональна, то розв'язок отримується поділом компонентів вектора b на діагональні елементи матриці. Якщо матриця квадратна і стрічкова, то застосовується спеціальний алгоритм на основі методу Гауса. Якщо матриця A є трикутною або може бути приведена до трикутної матриці перестановкою рядків і стовпців, то система вирішується методом підстановки. Якщо матриця не є трикутною, але є симетричною і має позитивні діагональні елементи, то MATLAB намагається застосувати розкладання Холецького і розв'язати дві системи з трикутними матрицями.
Якщо матриця хессенбергова, але не розріджена, то застосовується зведення до системи з трикутною матрицею. Якщо матриця квадратна, але перераховані вище методи застосувати не вдалося, то використовується метод LU -розкладу.
Якщо A – прямокутна матриця, то використовується QR -розкладання, що враховує можливий розріджений характер матриці.
Таким чином, операція \ або функція mldivide представляють досить складний розв'язувач (solver). Операція \ не дозволяє користувачеві керувати процесом розв'язання. Крім того, на численні перевірки при розв'язуванні великих систем витрачається досить багато часу.
2. Метод оберненої матриці. Розв'язок СЛАР Ax=b знаходять у вигляді: x=A-1b.
Наприклад:
> > A=[1 4 1 3; 0 -1 3 -1; 3 1 0 2; 1 -2 5 1];
b=[1; 2; 3; 4];
> > x=A^(-1)*b
x =
1.1364
-0.0455
0.5909
-0.1818
3. Функція linsolve розв'язує СЛАР і дозволяє користувачеві вибрати метод розв'язування, описавши властивості матриці. У найпростішому випадку звернення до функції має вигляд
> > x = linsolve(A, b)
При такому виклику у разі квадратної матриці використовується LU-розкладання, а в разі прямокутної матриці – QR-розкладу. Для задання властивостей матриці використовується керуюча структура, яку позначимо opts (можна використовувати будь-яке припустиме ім'я): x = linsolve(A, b, opts). Структура може мати поля, що описують властивості матриці: LT – нижня трикутна матриця, UT – верхня трикутна, UHESS – хессенбергова, SYM – симетрична, POSDEF – позитивно визначена, RECT – прямокутна, TRANSA – функції передається транспонована матриця. Поля можуть приймати значення true або false. Можна задавати не всі поля. Допустимі поєднання значень полів керуючої структури можна знайти в довідковій системі MATLAB. Функція не перевіряє зазначені властивості матриці, що прискорює розв'язок, але може призвести до помилок при неправильному зазначенні її властивостей.
Наприклад: A = [1 2 3; 0 4 5; 0 0 6]; b = [6; 9; 6]; % задати true для поля UT (а всі інші false)opts.UT = true; opts.TRANSA = false; opts.LT = false; opts.UHESS = false; opts.SYM = false; opts.POSDEF = false; opts.RECT = false; % функція linsolve буде розглядати матрицю А як верхню трикутну x = linsolve(A, b, opts) Отримаємо розв'язок: x = 1 1 14. Розв'язування СЛАР з використанням функції rref – приведено-ступінчаста форма матриці (reduced row echelonform). Ступінчаста матриця – матриця, що має m рядків і n стовпців, у якої перші r діагональних елементів ненульові, r £ min(m, n), а елементи, що лежать нижче діагоналі, і елементи останніх m-r рядків дорівнюють нулю:
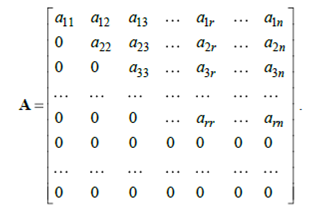
Функція R=rref() приводить матрицю до ступінчастої форми з використанням виключення Гауса-Жордана з вибором головного елемента по стовпцю.
Для того, щоб розв'язати СЛАР з квадратною неособливою матрицею A і вектором правої частини b, необхідно сформувати розширену матрицю, об'єднавши A і b, і використовуючи функцію rref, привести розширену матрицю до ступінчастого вигляду. Останній стовпець отриманої матриці є розв'язком системи.
Наприклад:
> > A = [1 -2 1; 2 -5 -1; -7 0 1];
> > B = [2; -1; -2];
> > R = rref([A b])
R =
1.0000 0 0 0.5200
0 1.0000 0 0.0800
0 0 1.0000 1.6400
5. Розв'язування СЛАР методом LU-розкладу або QR-розкладу.
Приклад розв'язування СЛАР методом LU-розкладу:
> > A=[1 4 1 3; 0 -1 3 -1; 3 1 0 2; 1 -2 5 1];
> > b=[1; 2; 3; 4];
> > [L, U]=lu(A)
L =
0.3333 1.0000 0 0
0 -0.2727 0.5806 1.0000
1.0000 0 0 0
0.3333 -0.6364 1.0000 0
U =
3.0000 1.0000 0 2.0000
0 3.6667 1.0000 2.3333
0 0 5.6364 1.8182
0 0 0 -1.4194
> > y=L\b
y =
3.0000
3.0000
0.2581
> > x=U\y
x =
1.1364
-0.0455
0.5909
-0.1818
Перевіримо правильність отриманого розв'язку:
> > b-A*x
ans =
1.0e-015 *
0.1110
-0.4441
0.4441
Приклад розв'язування СЛАР методом QR-розкладу:
> > [Q, R]=qr(A); y=Q'*b; x3=R\y
x3 =
1.1364
-0.0455
0.5909
-0.1818
6. Програмна реалізація одного з методів розв'язування СЛАР.
Розглянемо програмну реалізацію методу Гауса в Matlab. Створимо
m-файл:
function [x, flag]=gauss(A, b)
% реалізує метод Гауса з вибором головного елемента по стовпцю,
% використовується функція backsub розв'язку СЛАР з трикутною матрицею
% A - матриця nxn
% b - вектор правої частини
% x - вектор розв'язку
% flag – ознака виродження матриці A
% (flag=1 - матриця не вироджена, flag=0 - матриця вироджена)
% Ініціалізація вектора розв'язку x і тимчасового вектора C
[N, N]=size(A);
x=zeros(N, 1);
C=zeros(1, N+1); % тимчасовий вектор-рядок
B=[A b]; % розширена матриця
flag=1;
epsilon=1e-15; % величина для визначення виродження матриці A
% Прямий хід
for s=1: N % s - номер кроку
% Вибір головного елемента для неперетвореної частини стовпця p
% Y - максимальний елемент одновимірного масиву abs(B(s: N, s))
% j - номер максимального елемента в цьому масиві
[Y, j]=max(abs(B(s: N, s)));
% Міняємо місцями рядки s та j+s-1
C=B(s,:); % рядок s
B(s,:)=B(j+s-1,:);
B(j+s-1,:)=C;
if abs(B(s, s))< =epsilon
disp('Матриця A вироджена');
flag=0; % Ознака виродження матриці
break % Вихід із циклу
end
% Процес виключення для стовпця s
B(s, s: N+1)=B(s, s: N+1)/B(s, s);
for k=s+1: N
m=B(k, s)/B(s, s);
B(k, s: N+1)=B(k, s: N+1)-m*B(s, s: N+1);
end
end
if flag % Для невиродженої матриці
% Зворотний хід
x=backsub(B(1: N, 1: N), B(1: N, N+1));
end
Приклад розв'язування СЛАР методом Гауса з вибором головного елемента по стовпцях (використовуючи створену) функцію gauss().
clear;
clc;
% Приклад матриці і правої частини
disp('Матриця розв''язуваної системи')
A=[4 8 4 0
1 5 4 -3
1 4 7 2
1 3 0 -2]
disp('Вектор правої частини')
b=[ 8
-4
4]
[x, fl]=gauss(A, b); % Виклик методу Гауса
if fl
disp('Розв''язок')
x
disp('Нев''язка');
r=b-A*x
end
Приклад розв'язання системи з трьох лінійних рівнянь в MATLAB методом простих ітерацій.
clear, clc
A = [0 -0.06 0.02;
-0.03 0 0.05;
-0.01 -0.02 0];
B = [2; 3; 5];
% приводимо до нормального вигляду:
AB = [A B]; % розширена матриця
AB = AB([3 1 2],:) % переставляємо рядки
for i = 1: size(A)
a(i, 1: 3) = -AB(i, 1: 3)/AB(i, i);
a(i, i) = 0;
b(i, 1) = AB(i, 4)/AB(i, i);
end
a
b
eps = 1e-6; % точність чисельного розв'язку
X0 = b; % початкове наближення
X1 = a*X0+b;
iter=1;
while norm(X1-X0)> eps
X0 = X1;
X1 = a*X0+b;
iter=iter+1;
end;
disp('Розв''язок')
X = X1
disp('Кількість ітерацій: ')
iter
Отримаємо:
AB =
-0.0100 -0.0200 0 5.0000
0 -0.0600 0.0200 2.0000
-0.0300 0 0.0500 3.0000
a =
0 -2.0000 0
0 0 0.3333
0.6000 0 0
b =
-500.0000
-33.3333
60.0000
Розв'язок
X =
-338.0952
-80.9524
-142.8571
Кількість ітерацій:
iter =
Нев'язка:
> > B-A*X
ans =
1.0e-008 *
0.3518
0.5278
0.8796
Отже, розв'язок системи знайдено правильно із заданою точністю.
|
|