Представление целых чисел

Содержание учебного материала

Начальное понятие числа.

2. Представление целых чисел.

3. Специфические особенности вычислительной математики.

3.1. Обусловленность задачи.

3.2. Влияние выбора вычислительного алгоритма на результаты вычислений.

3.3. Экономичность вычислительного метода.

3.4. Погрешность метода.

4. Список рекомендуемой литературы.

Поршнев С.В., Беленкова И.В. Численные методы на базе Mathcad, стр. 10-14

Начальное понятие числа

Число—важнейшее понятие математики, которое складывалось и развивалось в течение длительного периода истории человечества. Люди начали работать с числами еще с первобытных времен. Первоначально человек оперировал лишь целыми положительными числами, которые называются натуральными числами: 1, 2, 3, 4, … Долго существовало мнение о том, что есть самое большое число, “боле сего несть человеческому уму разумевати” (так писали в старославянских математических трактатах).

Развитие математической науки привело к выводу, что самого большого числа нет. С математической точки зрения ряд натуральных чисел бесконечен, т.е. неограничен. С появлением в математике понятия отрицательного числа (Р.Декарт, XVII век в Европе; в Индии значительно раньше) оказалось, что множество целых чисел неограниченно как “слева”, так и “справа”. Математическое множество целых чисел дискретно и неограниченно (бесконечно).

Понятие вещественного (или действительного) числа в математику ввел Исаак Ньютон в XVIII веке. С математической точки зрения множество вещественных чисел бесконечно и непрерывно. Оно включает в себя множество целых чисел и еще бесконечное множество нецелых чисел. Между двумя любыми точками на числовой оси лежит бесконечное множество вещественных чисел. С понятием вещественного числа связано представление о непрерывной числовой оси, любой точке которой соответствует вещественное число.

Далее будет говориться об особенностях представления чисел в вычислительных устройствах: компьютерах, калькуляторах.

Представление целых чисел

В памяти компьютера числа хранятся в двоичной системе счисления. Есть две формы представления целых чисел в компьютере: целые без знака и целые со знаком.

Целые без знака — это множество положительных чисел в диапазоне [0, 2 k –1], где k — это разрядность ячейки памяти, выделяемой под число. Например, если под целое число выделяется ячейка памяти размером в 16 разрядов (2 байта), то самое большое число будет таким:

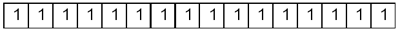
В десятичной системе счисления это соответствует: 2¹⁶ – 1 = 65 535

Если во всех разрядах ячейки нули, то это будет ноль. Таким образом, в 16-разрядной ячейке помещается 2¹⁶ = 65 536 целых чисел.

Целые числа со знаком — это множество положительных и отрицательных чисел в диапазоне [–2 ^{k –1}, 2 ^{k –1} – 1]. Например, при k = 16 диапазон представления целых чисел: [–32 768, 32 767]. Старший разряд ячейки памяти хранит знак числа: 0 — число положительное, 1 — число отрицательное. Самое большое положительное число 32 767 имеет следующее представление:

Например, десятичное число 255 после перевода в двоичную систему счисления и вписывания в 16-разрядную ячейку памяти будет иметь следующее внутреннее представление:

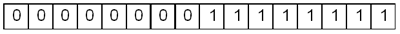
Отрицательные целые числа представляются в дополнительном коде. Дополнительный код положительного числа N — это такое его двоичное представление, которое при сложении с кодом числа N дает значение 2 ^k. Здесь k — количество разрядов в ячейке памяти. Например, дополнительный код числа 255 будет следующим:

Это и есть представление отрицательного числа –255. Сложим коды чисел 255 и –255:

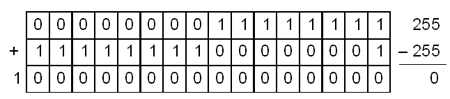
Единичка в старшем разряде “выпала” из ячейки, поэтому сумма получилась равной нулю. Но так и должно быть: N + (– N) = 0. Процессор компьютера операцию вычитания выполняет как сложение с дополнительным кодом вычитаемого числа. При этом переполнение ячейки (выход за предельные значения) не вызывает прерывания выполнения программы. Это обстоятельство программист обязан знать и учитывать!

Формат представления вещественных чисел в компьютере называется форматом с плавающей точкой. Вещественное число R представляется в виде произведения мантиссы m на основание системы счисления n в некоторой целой степени p, которую называют порядком: R = m * n^p.

Представление числа в форме с плавающей точкой неоднозначно. Например, для десятичного числа 25, 324 справедливы следующие равенства:

25, 324 = 2, 5324 * 10¹ = 0, 0025324 * 10⁴ = 2532, 4 * 10^–2 и т.п.

Чтобы не было неоднозначности, договорились в ЭВМ использовать нормализованное представление числа в форме с плавающей точкой. Мантисса в нормализованном представлении должна удовлетворять условию: 0, 1 _n 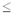m < 1 _n. Иначе говоря, мантисса меньше единицы и первая значащая цифра — не ноль. В некоторых случаях условие нормализации принимают следующим: 1 _n 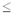m < 10 _n.

В памяти компьютера мантисса представляется как целое число, содержащее только значащие цифры (0 целых и запятая не хранятся). Следовательно, внутреннее представление вещественного числа сводится к представлению пары целых чисел: мантиссы и порядка.

В разных типах компьютеров применяются различные варианты представления чисел в форме с плавающей точкой. Рассмотрим один из вариантов внутреннего представления вещественного числа в четырехбайтовой ячейке памяти.

В ячейке должна содержаться следующая информация о числе: знак числа, порядок и значащие цифры мантиссы.

В старшем бите 1-го байта хранится знак числа: 0 обозначает плюс, 1 — минус. Оставшиеся 7 бит первого байта содержат машинный порядок. В следующих трех байтах хранятся значащие цифры мантиссы (24 разряда).

В семи двоичных разрядах помещаются двоичные числа в диапазоне от 0000000 до 1111111. Значит, машинный порядок изменяется в диапазоне от 0 до 127 (в десятичной системе счисления). Всего 128 значений. Порядок, очевидно, может быть как положительным, так и отрицательным. Разумно эти 128 значений разделить поровну между положительными и отрицательными значениями порядка: от –64 до 63.

Машинный порядок смещен относительно математического и имеет только положительные значения. Смещение выбирается так, чтобы минимальному математическому значению порядка соответствовал ноль.

Связь между машинным порядком (Mp) и математическим (p) в рассматриваемом случае выражается формулой: Mp = p + 64.

Полученная формула записана в десятичной системе. В двоичной системе формула имеет вид: Mp₂ = p₂ + 100 0000₂.

Для записи внутреннего представления вещественного числа необходимо:

1) перевести модуль данного числа в двоичную систему счисления с 24 значащими цифрами,

2) нормализовать двоичное число,

3) найти машинный порядок в двоичной системе счисления,

4) учитывая знак числа, выписать его представление в четырехбайтовом машинном слове.

Пример. Записать внутреннее представление числа 250, 1875 в форме с плавающей точкой.

Решение

1. Переведем его в двоичную систему счисления с 24 значащими цифрами:

250, 1875₁₀ = 11111010, 0011000000000000₂.

2. Запишем в форме нормализованного двоичного числа с плавающей точкой:

0, 111110100011000000000000 Ч 10₂¹⁰⁰⁰.

Здесь мантисса, основание системы счисления
(2₁₀ = 10₂) и порядок (8₁₀ = 1000₂) записаны в двоичной системе.

3. Вычислим машинный порядок в двоичной системе счисления:

Mp₂ = 1000 + 100 0000 = 100 1000.

4. Запишем представление числа в четырехбайтовой ячейке памяти с учетом знака числа

Шестнадцатеричная форма: 48FA3000.

Диапазон вещественных чисел значительно шире диапазона целых чисел. Положительные и отрицательные числа расположены симметрично относительно нуля. Следовательно, максимальное и минимальное числа равны между собой по модулю.

Наименьшее по абсолютной величине число равно нулю. Наибольшее по абсолютной величине число в форме с плавающей точкой — это число с самой большой мантиссой и самым большим порядком.

Для четырехбайтового машинного слова таким числом будет:

0, 111111111111111111111111 · 10₂^1111111.

После перевода в десятичную систему счисления получим:

MAX = (1 – 2^–24) · 2⁶³ 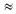10¹⁹.

Если при вычислениях с вещественными числами результат выходит за пределы допустимого диапазона, то выполнение программы прерывается. Такое происходит, например, при делении на ноль, или на очень маленькое число, близкое к нулю.

Вещественные числа, разрядность мантиссы которых превышает число разрядов, выделенных под мантиссу в ячейке памяти, представляются в компьютере приближенно (с “обрезанной” мантиссой). Например, рациональное десятичное число 0, 1 в компьютере будет представлено приближенно (округленно), поскольку в двоичной системе счисления его мантисса имеет бесконечное число цифр. Следствием такой приближенности является погрешность машинных вычислений с вещественными числами.

Вычисления с вещественными числами компьютер выполняет приближенно. Погрешность таких вычислений называют погрешностью машинных округлений.

Множество вещественных чисел, точно представимых в памяти компьютера в форме с плавающей точкой, является ограниченным и дискретным. Дискретность является следствием ограниченного числа разрядов мантиссы, о чем говорилось выше.

Количество вещественных чисел, точно представимых в памяти компьютера, можно вычислить по формуле: N = 2 ^t · (U – L + 1) + 1. Здесь t — количество двоичных разрядов мантиссы; U — максимальное значение математического порядка; L — минимальное значение порядка. Для рассмотренного выше варианта представления (t = 24, U = 63,
L = –64) получается: N = 2 146 683 548.

Пример 1. Получить внутреннее представление в формате “со знаком” целого числа 1607 в двухбайтовой ячейке памяти.

Решение

1) Перевести число в двоичную систему счисления: 1607₁₀ = 11001000111₂.

2) Дописывая слева нули до 16 разрядов, получим внутреннее представление этого числа в ячейке:

Желательно показать, как для сжатой формы записи этого кода используется шестнадцатеричная форма, которая получается заменой каждой четверки двоичных цифр одной шестнадцатеричной цифрой: 0647 (см. “ Системы счисления ” 2).

Более сложной является задача получения внутреннего представления отрицательного целого числа (– N) — дополнительного кода. Нужно показать ученикам алгоритм этой процедуры:

1) получить внутреннее представление положительного числа N;

2) получить обратный код этого числа заменой 0 на 1 и 1 на 0;

3) к полученному числу прибавить 1.

Пример 2. Получить внутреннее представление целого отрицательного числа –1607 в двухбайтовой ячейке памяти.

Решение

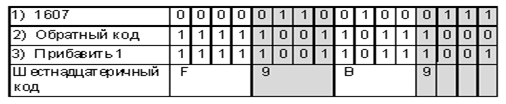
Полезно показать ученикам, как выглядит внутреннее представление самого маленького отрицательного числа. В двухбайтовой ячейке это –32 768.

1) легко перевести число 32 768 в двоичную систему счисления, поскольку 32 768 = 2¹⁵. Следовательно, в двоичной системе это:

2) запишем обратный код:

3) прибавим единицу к этому двоичному числу, получим

Единичка в первом бите обозначает знак “минус”. Не нужно думать, что полученный код