
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Подстановки.
|
|
В этом и нескольких следующих параграфах рассмотрим специальные классы функций: подстановки, размещения и сочетания. Эти функции часто используются. Особо отметим их приложения к теории графов, к трассировке вычислений и вообще работе программ, к построению языков программирования и переводу, к машинной графике.
Определение 1: Биективное отображение конечного множества А на себя называется подстановкой множества А.
Мы знаем, что биективное отображение любого множества А на себя называется преобразованием множества А. Поэтому определение подстановки можно сформулировать и так:
Определение 1’: Преобразование конечного множества А называется подстановкой множества А.
Если |A|=nÎ N, то можно решить вопрос о количестве различных подстановок множества А. Обозначим число таких подстановок через 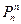 (читается: Р из n по n). Задачу построения биекции А на А можно рассматривать как задачу размещения n объектов (элементов множества А) по n ящикам, по одному в каждый ящик. Пронумеруем ящики от 1 до n. Порядок, в котором заполняются ящики, несуществен (любой другой порядок можно получить перемешиванием ящиков). Первый ящик может быть заполнен n способами, т.к. мы имеем свободный выбор из всего множества А. Убирая выбранный элемент из А, получим множество из n- 1 элементов. Следовательно, второй ящик может быть заполнен n- 1 способами, третий- n- 2 способами и т.д. Продолжая этот процесс, получим, что (n- 1)- й ящик может быть заполнен двумя способами, а ящик с номером n- единственным оставшимся элементом из А. Следовательно, число различных подстановок множества А равно n.(n- 1).(n- 2).....3.2.1. Это произведение называется факториалом числа n и обозначается n! Таким образом,
(читается: Р из n по n). Задачу построения биекции А на А можно рассматривать как задачу размещения n объектов (элементов множества А) по n ящикам, по одному в каждый ящик. Пронумеруем ящики от 1 до n. Порядок, в котором заполняются ящики, несуществен (любой другой порядок можно получить перемешиванием ящиков). Первый ящик может быть заполнен n способами, т.к. мы имеем свободный выбор из всего множества А. Убирая выбранный элемент из А, получим множество из n- 1 элементов. Следовательно, второй ящик может быть заполнен n- 1 способами, третий- n- 2 способами и т.д. Продолжая этот процесс, получим, что (n- 1)- й ящик может быть заполнен двумя способами, а ящик с номером n- единственным оставшимся элементом из А. Следовательно, число различных подстановок множества А равно n.(n- 1).(n- 2).....3.2.1. Это произведение называется факториалом числа n и обозначается n! Таким образом,
Pnn= n! = 1.2.3.... . (n- 1). n
Изучим теперь сами подстановки множества А и некоторые их свойства.
Поскольку А ~ Nn, то количество подстановок у них одно и тоже, Значит между множеством всех подстановок множества А и множеством всех подстановок множества Nn можно установить взаимно- однозначное соответствие (биекцию), т.е. каждой подстановке множества А соответствует единственная подстановка множества Nn и каждой подстановке множества Nn соответствует единственная подстановка множества А. Поэтому будем изучать подстановки Nn, которые будем обозначать буквами греческого алфавита.
Пусть y подстановка на Nn. Тогда y можно определить как множество пар следующим образом:
y= {(1, x1), (2, x2),..., (n, xn)}, где {x1, x2,..., xn} = Nn.
Не обязательно, конечно, x1= 1, x2= 2 и т.д.
Подстановки удобно записывать следующим образом:
y = 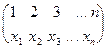 - здесь сразу видно какой элемент в какой переходит.
- здесь сразу видно какой элемент в какой переходит.
Пример 1: Пусть s- подстановка на N 6:
s= 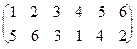 . Тогда s(1) = 5, s(2) = 6, s(3) = 3 и т.д.
. Тогда s(1) = 5, s(2) = 6, s(3) = 3 и т.д.
Достоинством этого обозначения является простота, с которой могут быть вычислены композиции подстановок. Разберем это на примере:
Пример 2: Пусть s подстановка из примера 1, а
r= 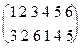 . Вычислим r
. Вычислим r  s: К каждому элементу N 6 применим сначала s, а потом к результату применим r: s(1)= 5, r(5)= 4, значит r(s(1))=4; s(2)= 6, а r(6)= 5, значит r(s(2))= 5 и т.д. В конечном итоге получаем r
s: К каждому элементу N 6 применим сначала s, а потом к результату применим r: s(1)= 5, r(5)= 4, значит r(s(1))=4; s(2)= 6, а r(6)= 5, значит r(s(2))= 5 и т.д. В конечном итоге получаем r  s =
s = 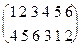 .
.
Композицию подстановок можно построить и так: переставим в подстановке r столбцы так, чтобы ее первая строка была такой же как и вторая строка в подстановке s
r= 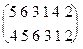 и запишем их одна под другой:
и запишем их одна под другой:
s= 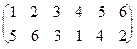
r= 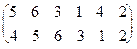 , тогда легко получаем
, тогда легко получаем
r  s =
s = 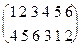 .
.
s  r =
r = 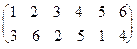 , значит r
, значит r  s ¹ s
s ¹ s  r.
r.
Пример 3: Пусть s- подстановка из примера 1. Найти s10, т.е. s  s
s  s
s  ...
...  s - 10 раз.Для этого вовсе не обязательно находить десять раз образы каждого элемента. Замечаем, что s(1)= 5, s(5)= 4, s(4)= 1, значит s3(1)= 1, но s10= s
s - 10 раз.Для этого вовсе не обязательно находить десять раз образы каждого элемента. Замечаем, что s(1)= 5, s(5)= 4, s(4)= 1, значит s3(1)= 1, но s10= s  s3
s3  s3, значит s10(1)= 5. Далее:
s3, значит s10(1)= 5. Далее:
s2(2)= 2 Þ s10(2)= 2,
s10(3)= 3,
s3(4)= 4 Þ s10(4)= 1,
s3(5)= 5 Þ s10(5)= 4,
s2(6)= 6 Þ s10(6)= 6.
В итоге получаем: s! 0= 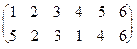 .
.
Определение 2: Подстановка  называется тождественной подстановкой и обозначается In (т.к. I Nn -слишком громоздко).
называется тождественной подстановкой и обозначается In (т.к. I Nn -слишком громоздко).
Поскольку подстановка это биекция, имеет смысл говорить об обратной подстановке. Как построить обратную подстановку? Учитывая свойство биекции s  s-1 = In= s-1
s-1 = In= s-1  s: Если s переводит k в ak, то s-1 должна ak перевести в k. Поэтому получаем правило построения s-1 из s:
s: Если s переводит k в ak, то s-1 должна ak перевести в k. Поэтому получаем правило построения s-1 из s:
Подстановка s-1 получается из s перестановкой строк.
Пример 4: Пусть r- подстановка из примера 2. Тогда
r-1= 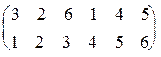 . Перепишем ее в более удобном виде:
. Перепишем ее в более удобном виде:
r-1= 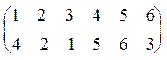 . Тогда
. Тогда
r-1  r =
r = 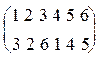
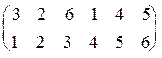 =
=  = I6.
= I6.
r  r-1 =
r-1 = 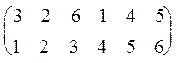
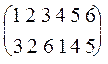 =
=  = I6.
= I6.
Хотя рассмотренное выше представление подстановок удобно для вычислений, однако, оно требует много лишнего места, особенно в тех случаях, когда многие элементы не меняются в процессе подстановки. Приведем другое, более простое представление, которое позволит получить нам одно весьма полезное свойство подстановок.
Определение 3: Пусть A = {a1, a2,..., an} (т. е. элементы множества пронумерованы каким - то образом). Подстановку w называют циклом (циклической подстановкой), если ее можно представить в виде:
w = 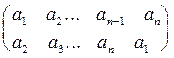 .
.
Предположим теперь, что AÍ B и |B|= m³ n. Зададим подстановку c на В, расширяя подстановку  , так, что
, так, что
c: x 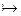
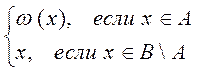
Т.е. если B = {a1, a2, ..., an, an+1,..., am}, то c можно записать в виде:
c = 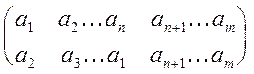 (1)
(1)
|
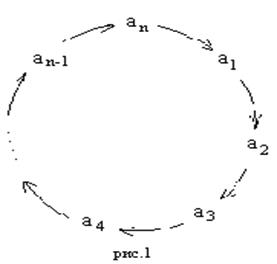
Подстановка c, действуя на В, ведет себя как  , во всех тех случаях, когда элементы В не остаются на месте. Можно сказать, что c передвигает элементы ai циклическим образом («по кругу» см. рис.1).
, во всех тех случаях, когда элементы В не остаются на месте. Можно сказать, что c передвигает элементы ai циклическим образом («по кругу» см. рис.1).
Поскольку, как правило, множество, на котором действует подстановка известно (для c это В), то ее удобно записывать в следующей форме:
c= (a1, a2,..., an) (2)
Эта подстановка называется циклом длины n. Цикл длины 1 будем называть тривиальным циклом. Поэтому можно сказать, что (2) получена из (1) исключением циклов длины 1. С другой стороны если подстановка c задана в виде (2), то легко понять, как она действует на B (рис. 2).

И ее легко записать в виде (1). Т.е. при переходе от (2) к (1) мы добавляем циклы длины 1, если они есть.
Пример 5. Рассмотрим опять подстановку r = 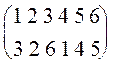 . Перепишем ее в виде (1) r =
. Перепишем ее в виде (1) r = 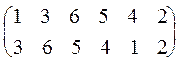 , т.е. эта подстановка является циклом длины 5 и ее можно представить в виде r = (1, 3, 6, 5, 4). Не все подстановки, конечно же, являются циклом, однако они все содержат циклы.
, т.е. эта подстановка является циклом длины 5 и ее можно представить в виде r = (1, 3, 6, 5, 4). Не все подстановки, конечно же, являются циклом, однако они все содержат циклы.
Пример 6. Подстановка s из примера 1 s = 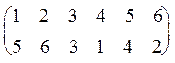 .
.
Ее можно представить в виде: s = 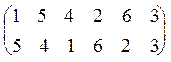 . Как видно, она сама не является циклом, но содержит два нетривиальных цикла: (1, 5, 4) и (2, 6). Для того чтобы понять, что собой представляет s дополним каждый из этих циклов до преобразования N6, не забыв о тривиальном цикле (3), и представим их в форме (1). А именно:
. Как видно, она сама не является циклом, но содержит два нетривиальных цикла: (1, 5, 4) и (2, 6). Для того чтобы понять, что собой представляет s дополним каждый из этих циклов до преобразования N6, не забыв о тривиальном цикле (3), и представим их в форме (1). А именно:
s1= (1, 5, 4)= 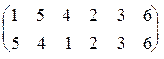 ; s2 = (2, 6) =
; s2 = (2, 6) =  , тогда
, тогда
s2  s1 =
s1 =  ; s1
; s1  s2 =
s2 = 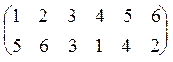 . Мы видим, что s = s1
. Мы видим, что s = s1  s2 = s2
s2 = s2  s1 (*)
s1 (*)
Нам удалось представить подстановку множества, состоящего из шести элементов в виде композиции двух нетривиальных циклов. В этом случае будем говорить, что подстановка s представлена в виде произведения двух циклов и записывать s = (1, 5, 4) (2, 6).
Из того, что s- биекция и по основному свойству биекций:
f (X Ç Y) = f (X) Ç f (Y), можно сделать вывод, что циклы одной и той же подстановки не могут содержать общие элементы. Следовательно, подстановку s мы представили в виде произведения непересекающихся циклов.
На самом деле имеет место общая теорема:
Теорема (о представлении подстановки). Всякая подстановка конечного множества может быть представлена в виде произведения не пересекающихся циклов.
(без доказательства), желающие могут найти его в книге [1].
Вернемся к примеру 5. Равенство (*) говорит нам о том, что если s1 и s2 не пересекающиеся циклы одной подстановки s, то s1  s2 = s2
s2 = s2  s1, что неверно для произвольных подстановок. Значит, циклы обладают какими- то свойствами, которыми не обладают произвольные подстановки конечных множеств. Попробуем сформулировать их и, по- возможности доказать.
s1, что неверно для произвольных подстановок. Значит, циклы обладают какими- то свойствами, которыми не обладают произвольные подстановки конечных множеств. Попробуем сформулировать их и, по- возможности доказать.
Свойство 1: Композиция (произведение) циклов одной и той же подстановки коммутативна. (Доказательство самостоятельно).
Свойство 2: Если k- длина цикла w, то wk = 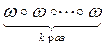 =Ik, т.е. тождественная подстановка.
=Ik, т.е. тождественная подстановка.
Доказательство: Идея: w = (а1, а2,..., аk) - цикл. Чтобы а1 перевести в аk понадобится подстановка  k-1, а значит, чтобы аk перевести в а1 понадобится
k-1, а значит, чтобы аk перевести в а1 понадобится 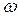 k.
k.
Учитывая свойства 1 и 2, задачу, поставленную в примере 3, можно было бы решить быстрее:
s = (1, 5, 4) (2, 6), при этом, учитывая обозначения примера 6, имеем:
s = s1  s2, значит s10= (s1
s2, значит s10= (s1  s2)10 = учтем свойство 1 и ассоциативность композиции = s110
s2)10 = учтем свойство 1 и ассоциативность композиции = s110  s210 . Значит, по свойству 2, через три шага 1, 5 и 4 перейдет в себя, а значит через 10 шагов 1
s210 . Значит, по свойству 2, через три шага 1, 5 и 4 перейдет в себя, а значит через 10 шагов 1 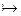 5, 5
5, 5 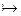 4, 4
4, 4 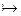 1. Через два шага двойка и шестерка перейдут в себя. Значит через 10 шагов 2
1. Через два шага двойка и шестерка перейдут в себя. Значит через 10 шагов 2 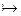 2, 6
2, 6 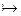 6. Ну а тройка всегда переходит сама в себя (ведь s- это подстановка на N6). Значит
6. Ну а тройка всегда переходит сама в себя (ведь s- это подстановка на N6). Значит
s10 = 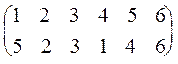 = (1, 5, 4) - это цикл длины 3.
= (1, 5, 4) - это цикл длины 3.
§ 7. Отображение конечных множеств (продолжение).
Рассмотрим теперь несколько иную ситуацию. Пусть А- конечное множество и |A| = n, B Í A, |B| = r £ n. Возникает вопрос: сколько существует биективных функций из A на B? Или, что эквивалентно: сколько существует инъективных отображений В в А? Попробуем ответить на этот вопрос, используя снова ситуацию размещения n предметов по r ящикам. В первый ящик мы можем положить n предметов, во второй - n-1 и т.д., в r-й - n-r+1. Получаем некоторое число, которое, учитывая аналогию с подстановками, обозначим
Pnr = n (n – 1)... (n – r + 1) (1)
Число Pnr показывает, сколько кортежей (упорядоченных наборов) длины r можно построить из элементов n - элементного множества А.
Определение 1: Упорядоченное r-элементное подмножество n-элементного множества будем называть размещением (без повторений) из n элементов по r.
Для общности приведем (1) к несколько иному виду: умножим и разделим правую часть на (n - r)!:
Pnr = 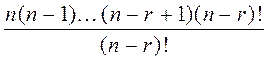 =
= 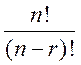 (2)
(2)
Однако при постановке задачи мы брали r £ n, а оно у нас в знаменателе. Поэтому поступим так положим 0! = 1. Для этого есть основания - на множестве из k элементов существует k! подстановок. А сколько подстановок на Æ? Разумно предположить, что есть единственная биекция Æ на себя! Теперь формула (2) и обозначение Pnr согласуется с нашим предыдущим обозначением, а именно Pnr = 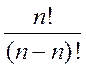 = n!
= n!
Откажемся теперь от «упорядоченности» множества В.
Определение 2. Пусть В Í А и | A | = n, | B | = r, r £ n. Подмножество (неупорядоченное) В называется сочетанием из n элементов по r. Число таких сочетаний обозначается Cn r.
Попробуем найти формулу для нахождения числа Cnr. Сколькими способами можно выбрать r элементов из n- элементного множества? Или: Сколько существует биективных функций из А на В. Имеющих В своим образом?
Пусть f и g две такие функции. Ef= Eg= B. Как связаны друг с другом эти функции? Для ответа на этот вопрос рассмотрим диаграммы:
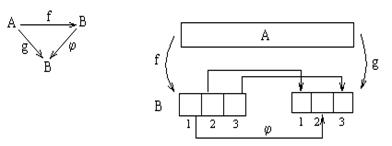
Т.е. j должно быть биекцией В на В такой, что g= j  f. А значит число таких функций равно числу подстановок множества В, т.е. Prr. А всего способов отображения А на В - Pnr. В итоге получаем формулу количества размещений(без повторений) из n элементов по r:
f. А значит число таких функций равно числу подстановок множества В, т.е. Prr. А всего способов отображения А на В - Pnr. В итоге получаем формулу количества размещений(без повторений) из n элементов по r:
Pnr= Cnr. Prr (3) Отсюда
Cnr= 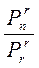 =
= 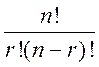 (4)
(4)
Если отвлечься от поставленной задачи и изучить сами числа Cnr, определяемые формулой (3), то можно заметить некоторые интересные свойства:
Свойство 1 (симметрия):
Cnr= Cnn-r.
Доказательство:
Cnn-r= 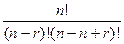 =
= 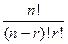 = Cnr.
= Cnr.
Комментарий: Если r- элементное подмножество В n- элементного множества А можно выбрать несколькими способами, то дополнение А\В можно выбрать таким же числом способов.
Свойство 2 (Правило Паскаля):
Cn+1r = Cnr + Cnr-1.
Доказательство:
Cnr + Cnr-1= 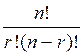 +
+ 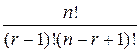 =
= 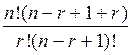 =
=
=  =
= 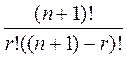
Что и требовалось доказать.
Это дает рекуррентный способ построения чисел Cnr. Только надо доопределить для r = 0: Cn0 = 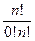 = 1= Cnn (по свойству 1). Попробуем расположить наши результаты в виде таблицы. Будем располагать в n строках, т.е. номер строки равен n, а номер столбца равен r, а еще нулевой столбец и строку:
= 1= Cnn (по свойству 1). Попробуем расположить наши результаты в виде таблицы. Будем располагать в n строках, т.е. номер строки равен n, а номер столбца равен r, а еще нулевой столбец и строку:
| r n | |||||
Чаще эту таблицу записывают в следующем виде, где проще просматривается закономерность получения элементов каждой следующей строки из предыдущей:
1 1
1 2 1
1 3 3 1
1 4 6 4 1
.............
Свойство 3(бином Ньютона). Для любых действительных чисел а и b и для любого натурального числа n имеет место формула:
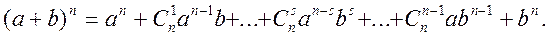 .
.
Замечание: Если учесть, что Cn0 = Cnn, и a n = Cn0 an b0,
bn = Cnn a0 bn , то бином запишется так: (a + b) n =  .
.
Доказательство (по индукции):
I шаг. При n= 1: a+ b= C10a+ C11b= a+ b.
II шаг. Пусть (a+ b)k= 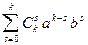 - верно. Тогда (a+b)k+1= (a+b)k(a+b)=
- верно. Тогда (a+b)k+1= (a+b)k(a+b)= 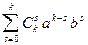 . (a+b)=
. (a+b)= 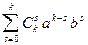 a +
a + 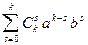 b= ak+1 + (Ck0+ Ck1)akb + (Ck1+ Ck2)ak-1b2 +...+ (Cks+ Cks+1)ak-sbs+...+ bk+1, получаем (по свойству 2: Cks+Cks+1= Ck+1s+1):
b= ak+1 + (Ck0+ Ck1)akb + (Ck1+ Ck2)ak-1b2 +...+ (Cks+ Cks+1)ak-sbs+...+ bk+1, получаем (по свойству 2: Cks+Cks+1= Ck+1s+1):
(а+ b)k+1= ak+1+ Ck+11akb+ Ck+12ak-1b2+...+ Ck+1s+1ak-sbs+1+...+ bk+1. Ч.т.д.
Поэтому числа Cnr называются биномиальными коэффициентами.
Какие задачи можно решать, используя введенные в начале параграфа понятия? Задачи на определение числа возможных конечных множеств или кортежей с заданными свойствами, которые можно составить из элементов данного конечного множества, или числа возможных функций (или отношений) с заданными свойствами, которые можно построить между двумя конечными множествами. Такие задачи обычно называют комбинаторными задачами.
Рассмотрим некоторые такие задачи (на конкретных множествах).
Пример 1: Клавиатура пианино содержит 88 клавиш. Сколько различных музыкальных фраз можно составить из 6 нот, если не допускать в одной фразе одинаковых звуков?
P886= 88.87.86.85.84.83= 390 190 489 920.
Специально было сказано: «без повторений». Это словосочетание уже звучало в определениях 1 и 2. Попробуем отказаться от него.
Пример 2: Сколько различных музыкальных фраз можно составить из 6 нот, допуская повторение одних и тех же звуков?
Эта задача тоже на построение кортежа длины 6. Но отличается от предыдущей тем, что после выбора первой ноты для выбора второй имеется снова 88 возможностей. Таким образом общее число фраз равно
886= 464 404 086 784= R886.
В общем виде эту задачу можно сформулировать так: |A|= n. Сколько кортежей с повторениями длины k можно составить из элементов А? Эта задача равносильна следующей: Найти |Ak|, если |A|= n. По теореме о мощности прямого произведения |Ak|= nk. Т.е. число размещений с повторениями из n элементов по k равно Rnk= nk.
Пример 3: В университете есть 60 человек играющих в футбол. Из них надо составить 3 команды, т.е. отобрать 33 человека. Остальные 27 человек будут в запасе.
Решение: С6033 = С6027 - это более, чем миллиард миллиардов.
На самом деле существует много комбинаторных задач, в которых невозможно указать простую формулу для числа допускаемых задачей логических возможностей. В некоторых из них может оказаться полезным общий принцип.
Принцип умножения: Пусть некоторый выбор может быть сделан в точности r различными способами; для каждого их этих способов некоторый второй выбор может быть сделан в точности s различными способами; для каждой пары первых двух выборов некоторый третий выбор может быть сделан в точности t способами и т.д. Тогда число способов для последовательности этих выборов получается перемножением соответствующих чисел, т.е. равно r . s . t×....
(Можно проверить на множестве, состоящем из 3 или 4 элементов).
Прежде чем привести следующий пример, дадим удобное определение.
Определение: Размещение из n элементов по n будем называть перестановкой n- элементного множества. Другими словами, перестановка- это образ n- элементного множества А при подстановке на А.
Число перестановок из n по n равно числу подстановок n- элементного множества, т.е. Pnn= n! = Pn.
Пример 4: (перестановки с повторениями). Имеется 3 одноцветные пешки и 2 одноцветных коня. Сколькими способами можно их расставить в ряд?
Наклеим на фигуры разноцветные ярлыки и будем временно считать все фигуры различными. Тогда число способов расстановки в ряд пяти фигур будет P5= 5! Но если теперь снять ярлыки, то среди 5! перестановок будут совпадающие. Совпадающими будут перестановки, отличающиеся порядком пешек, их всего P3= 3!, и порядком коней- их P2= 2! Значит общее число способов расстановки в ряд трех одноцветных пешек и 2 одноцветных коней равно 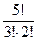 = 10.
= 10.
Можно обобщить эту задачу и показать, что число различных расположений n объектов, среди которых имеется n1 неразличимых объектов типа 1, n2 объектов типа 2 и т.д., nr объектов типа r равно:
Pn(n1, n2,..., nr)= 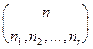 =
= 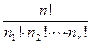 , где n1+ n2+...+ nr= n.
, где n1+ n2+...+ nr= n.
Общие рассуждения мало чем отличаются от рассуждения примера 4. Следующий пример иллюстрирует разнообразие комбинаторных задач и так или иначе использует способы рассуждений, приводившиеся выше.
|
|