Графический метод решения задачи линейного программирования при степени неопределенности равной двум

(самостоятельное изучение)

Итак, множество допустимых решений (многогранник решений) задачи линейного программирования представляет собой выпуклый многогранник (или выпуклую многогранную область), а оптимальное решение задачи всегда находится, по крайней мере, в одной из угловых точек этого многогранника.

Рассмотрим следующую основную задачу линейного программирования. Пусть заданы ограничения:

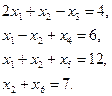(2.7)

и функция цели

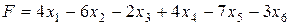. (2.8)

Требуется среди всех неотрицательных решений системы линейных уравнений получить такое, при котором функция F принимает наибольшее значение. Из анализа условий задачи следует:

1) целевая функция – линейная;

2) задача решается на максимум;

3) ограничения линейные и равенства;

4) неизвестных переменных – 6;

5) уравнений ограничений – 4.

Система является неопределенной и степень неопределенности

p = n – m = 6 – 4 = 2.

Получить однозначное решение такой задачи классическими методами не представляется возможным. Задачу с такой степенью неопределенности можно решить графическим методом. Покажем это на конкретном примере.

. Выберем в качестве базисных (основных) переменные х₃; х₄; х₅; х₆, в качестве свободных неосновных – х₁ и х₂.

Выразим основные переменные через неосновные и умножим первое уравнение на (-1). Получим систему уравнений:

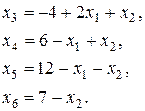(6.9)

Она имеет бесчисленное множество решений. Однако среди них необходимо выбрать только те, которые имеют неотрицательные решения этой системы. Поэтому дополним эти уравнения условиями неотрицательностии перепишем:

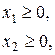
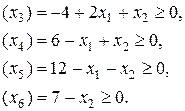(6.10)

Множество решений системы неравенств называют областью определения допустимых решений или просто областью допустимых решений данной ЗЛП.

Для этого введем систему координат х ₁ – 0 – х₂. Полагая, что в неравенствах крайний случай – знак равенства, получаем следующие уравнения:

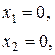
(2.11)

Этим уравнениям геометрически соответствуют прямые на плоскости х ₁ – 0 – х₂ , рисунок 2.2.

Каждая из прямых делит всю плоскость х ₁ – 0 – х₂ на две полуплоскости: координаты точек одной из них удовлетворяют соответствующему неравенству (эти направления указаны стрелками на линиях), а другой – не удовлетворяют. Эту оценку осуществим подстановкой в неравенства координат контрольной точки 0(0, 0).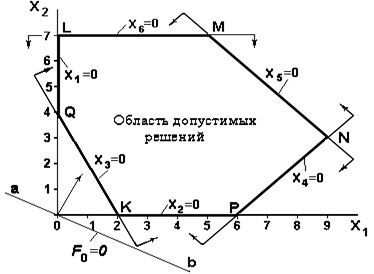

Рисунок 2.2- Графическая интерпретация решения задачи

линейного программирования

Очевидно, что область допустимых решений будет лежать внутри замкнутого многоугольника. Это многоугольник допустимых решений основной ЗЛП. Для рассматриваемого случая – многоугольник MNPKQL. На предыдущих лекциях мы показали, что такой многоугольник всегда выпуклый.

Координаты любой точки, лежащей как внутри этой области, так и на ее сторонах, будут удовлетворять условиям ограничений ЗЛП.

Однако задача заключается в том, чтобы среди этого бесчисленного множества возможных решений, получить такое, которое было бы оптимально, т.е. функция цели принимала наибольшее значение.

Выразим функцию цели через свободные неизвестные х₁ и х₂ , для чего в целевую функцию (2.8) подставим равенства (2.9) и в результате получим функцию:

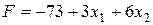. (2.12)

Очевидно, эта функция аргументов х₁ и х₂ в каждой точке многоугольника допустимых решений принимает определенное значение, и в какой-то, по крайней мере одной его точке, она примет наибольшее значение. Получим эту точку многоугольника, для чего введем в рассмотрение вспомогательную функцию:

; т.е. 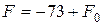. (6.13)

Функция F₀ отличается от тсходной лишь на постоянную величину, поэтому они будут иметь один и ту же точку экстремума, т.е. F₀ принимает наибольшее значение в той же точке многоугольника, что и функция F. Воспользуемся известной геометрической трактовкой функции двух переменных – линиями уровня.

Линии уровня – это геометрическое место точек, в которых функция принимает одно и то же значение. Пусть С - некоторое произвольное значение, принимаемое функцией F₀ . Тогда уравнение линии уровня, соответствующей этому значению, имеет вид:

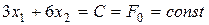
или относительно х₂ :

. (2.14)

Любая линия, имеющая коэффициент угла наклона k=(-1/2), будет отвечать уравнению (2.14). Но через каждую точку плоскости может проходить только одна линия уровня функции и среди них найдется такая, для которой будет соответствовать конкретное значение С (или, что одно и то же, F₀). Для другой точки, через которую пройдет линия уровней (т.е. в данном случае прямая с постоянным угловым коэффициентом k=(-1/2), будет другое значение F₀. Учитывая это, найдем среди всех точек многоугольника допустимых решений ту, через которую проходит линия уровня функции F₀ с ее наибольшим значением. Эта точка будет соответствовать оптимальному решению рассматриваемой ЗЛП.

Построим линию уровня, предполагая, что F₀=С=0. Это имеет место при х₁=0 и х₂=0, причем линия должна иметь угловой коэффициент k=(-1/2). На рисунке 6.1 это линия ab, проведенная через начало координат. Стрелкой указано направление, в котором будут располагаться линии уровня с более высокими значениями функции цели. Действительно, исходя из структуры функции F (2.12), видно, что чем больше будут принимать значение величины х₁ и х₂, тем больше будет функция цели F. Поэтому естественно линию функции F₀ надо перемещать вверх и вправо, и чем дальше она будет расположена от начала координат, тем больше значение функции цели. Тогда геометрически эта задача решается просто: необходимо перемещать линию уровней F₀=0 параллельно самой себе и определить крайнюю точку контакта этой линии и многоугольника области допустимых решений. В данном случае этому условию отвечает точка М, координаты которой получим, решая систему уравнений

,

.

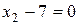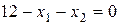Они равны х₁=5, х₂=7. Тогда нетрудно получить и остальные независимые величины: х₃=13; х₄=8; х₅=0; х₆=0, а соответственно и наибольшее значение функции цели F_мах= - 16.

Таким образом, основная ЗЛП с помощью геометрических построений решена. Очевидно, аналогичными геометрическими построениями может быть решена и любая другая основная ЗЛП, у которой ограничения имеют степень неопределенности р = 2.

Cформулируем последовательность действий, которую необходимо выполнить при решении любой другой подобной задачи.

1. Выбрать пару свободных (неосновных) переменных и определить оставшиеся основные (базисные) переменные.

2. Выразить основные переменные через неосновные.

3. Дополнить полученную систему неравенств условиями неотрицательности всех переменных.

4. Ввести систему координат (из пары неосновых переменных).

5. Формально перейти от системы ограничений неравенств к системе ограничений равенств.

6. Построить многоугольник решений.

7. Выразить функцию цели через неосновные (свободные) переменные.

8. Ввести вспомогательную функцию, отличающуюся от целевой только постоянной величиной.

9. Построить линию уровня.

10. Перемещать линию уровня в направлении возрастания вспомогательной функции до контакта с крайней точкой многоугольника решений.

11. Определить графически (аналитически) координаты этой точки, значения всех остальных переменных и значение в ней целевой функции.

Это и будет решением поставленной задачи.

Если после выполнения процедуры по п.6 получают незамкнутый многоугольник, то такая задача решения не имеет.

Однако необходимо отметить, что даже с учетом рассмотренного решения задачи ЛП графическим методом при числе переменных более двух, все равно возможности графического метода существенно ограничены (даже в данном случае неопределенность не может превышать двух), поэтому необходимо было разработать универсальный метод, позволяющий решать все (имеющие реальные исходные данные) задачи линейного программирования.

2.. Разработка обоснованных оптимальных решений в задачах нелинейного программирования методом множителей Лагранжа