
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Частотный метод определения автоколебаний
|
|
В НЕЛИНЕЙНОЙ САУ (практическое занятие 6)
Цель работы:
1) знакомство с особенностями существенно нелинейных САУ;
2) анализ нелинейной САУ с помощью уравнения замыкания и проверка результатов анализа методом моделирования.
Постановка задач исследования
Задана передаточная функция линейной инерционной части САУ: 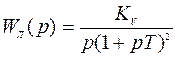 и ее параметры: T=21-№ , KV=1/T, где № - номер бригады.
и ее параметры: T=21-№ , KV=1/T, где № - номер бригады.
На входе линейной инерционной части САУ включен безынерционный нелинейный элемент - идеальное реле (с=1в).
Требуется найти решение уравнения замыкания (графическим способом), определить параметры автоколебаний в нелинейной САУ (амплитуду и частоту), после чего проверить результаты теоретического анализа методом моделирования.
Описание схемы моделирования
Схема моделирования приведена на рис.8 и содержит компоненты «DIFF», «HILO» и «LAPLACE» из библиотеки «Abm.slb». В атрибутах «HILO» указать верхний и нижний уровни ограничения: HI=1, LO=-1; в атрибутах «LAPLACE» задать передаточную функцию линейной части системы. Входное воздействие (генератор V1 типа «VPWL») положить равным единице.
Задание по экспериментальной части работы
В режиме «Transient» исследовать автоколебания в нелинейной САУ. Оценить амплитуду и частоту гармонического процесса.
Содержание отчета
1. Задание, графическое решение уравнения замыкания (годографы), расчет амплитуды и частоты автоколебаний.
2. Схема моделирования, списки соединений, директивы моделирования.
3. Результаты экспериментальных исследований (осциллограмма гармонического процесса и его параметры).
4. Заключение, содержащее постановку задач исследования, методику их проведения и основные выводы.
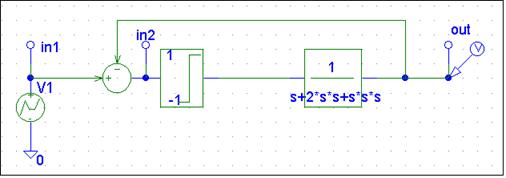
Рис.8
Контрольные вопросы
1. Сформулировать условие возникновения автоколебаний в нелинейной САУ.
2. Указать ограничения, при которых справедлив анализ автоколебаний в нелинейной САУ.
3. Возможно ли существование автоколебаний в нелинейной системе с интегратором и одним апериодическим звеном (ответ обосновать)?
4. Возможно ли существование автоколебаний в исследуемой системе, если реле имеет зону нечувствительности (b=0.1v; b=0.5v)?
5. Устойчива ли исследуемая система без нелинейного элемента (ответ обосновать)?
6. Какие изменения в параметры системы следует внести, чтобы амплитуда автоколебаний увеличилась?
7. Какие изменения в параметры системы следует внести, чтобы частота автоколебаний увеличилась?


Содержание
1. Возможности пакета DesignLab 8.0.и краткая инструкция для работы с ним............................. 3
2. Моделирование устройств радиоавтоматики методом замещения LCR-цепью (лабораторная работа 1)................. 5
3. Моделирование САУ с электронным интегратором
(лабораторная работа 2).................... 8
4. Коррекция систем (лабораторная работа 3)........... 10
5. Решение систем дифференциальных уравнений
(лабораторная работа 4)................... 12
6. Моделирование системы синхронизации
(лабораторная работа 5).................... 14
7. Частотный метод определения автоколебаний в нелинейной САУ
(лабораторная работа 6)................... 19
Список литературы
1. Коновалов Г.Ф. Радиоавтоматика. Учеб.для вузов по спец.Радиотехника, - М. Высш.шк. 2003. - 335с.
2. Первачев С.В. Радиоавтоматика. Учеб.для вузов, - М.- Радио и связь - 1982. - 296с.
3. Радиоавтоматика. Учеб.пособие для студ.вузов спец.Радиотехника /
В.А.Бесекерский, А.А.Елисеев, А.В.Небылов и др. Под ред.В.А.Бесекерского, - М.- Высш.шк., 1985. - 271с.
4. Бесекерский В. А., Попов Е. П. Теория систем автоматического регулирования. - М.: Наука, 1972. - 768 с.
5. Воронов А. А. Основы теории автоматического управления. - М.: Энергия. - Т. 1. - 1980. - 312 с.; Т. 2. - 1981. - 304 с.
6. Красовский А. А., Поспелов Г. С. Основы автоматики и технической кибернетики. - М.: ГЭИ, 1962. - 600 с.
7. Первачев С. В., Валуев А. А., Чиликин В. М. Статистическая динамика радиотехнических следящих систем. М.: Сов. радио, 1973. – 488 с.
8. Теория автоматического управления: В 2 ч. / Под ред. А. А. Воронова. - М.: Высш. шк., 1986. - Ч. 1 - 2. - 655 с.
9. Теорiя автоматичного управлiння / Г. Ф. Зайцев, В. К. Стеклов, О. I. Брiцький; За ред. проф. Г. Ф. Зайцева. – К.: Технiка, 2002. – 688 с.
10. Юревич Е. И. Теория автоматического управления. - Л.: Энергия. Ленингр. отд-ние, 1975. - 410 с.
11. Разевиг В.Д. Система схемотехнического моделирования и проектирования печатных плат Design Center (PSpice). - М., 1996.
Приложение. РАСЧЕТ ТОЧНОСТНЫХ ХАРАКТЕРИСТИК СИСТЕМЫ СИНХРОНИЗАЦИИ (задание Д)
Это дополнительное задание может быть рекомендовано студентам, желающим улучшить свое рейтинговое состояние.
Задана передаточная функция разомкнутой системы 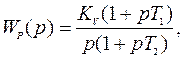
где KV=64/M; T2=M; T11=T2/16; T12=T2/4; 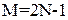 ;
;
N - порядковый номер студента в списке группы.
Структура системы должна быть согласована с формирующим фильтром (ФФ), вырабатывающим случайный процесс с экспоненциально-коррелированной скоростью (двусторонняя спектральная плотность мощности шума на входе ФФ - SO=642/M). Уход фазы синхронизирующего генератора наблюдается на фоне аддитивного белого шума (двусторонняя спектральная плотность мощности шума SП=M).
Требуется
1. Построить ЛХ и изобразить переходные процессы (два).
2. Изобразить структуру ФФ и согласованной с ним системы синхронизации. Описать систему в пространстве состояний, решить систему дифференциальных уравнений численным методом с помощью ЭВМ и построить переходные процессы (начальные условия - нулевые, входное воздействие - единичное). Сравнить результаты п.1 и п.2.
3. Записать линейное дисперсионное уравнение системы, представить его в виде системы дифференциальных уравнений, решить численным методом и построить зависимости дисперсий флюктуационной s2фл(t) и динамической s2g(t) составляющих ошибки системы от времени (выбрать начальное условие 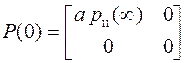 ,
, 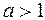 ).
).
4. С помощью частотных методов анализа систем рассчитать s2фл и s2g в установившемся режиме. Сравнить результаты п.3 и п.4.
|
|