
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Шкала Бофорта для измерения силы ветра
|
|
Сила Название Признаки
ветра,
 балл
балл
0 Штиль Дым идет вертикально
1 Тихий Дым идет слегка наклонно
2 Легкий Ощущается лицом, шелестят листья
3 Слабый Развеваются флаги
4 Умеренный Поднимается пыль
5 Свежий Вызывает волны на воде
6 Сильный Свистит в вантах, гудят провода
7 Крепкий На волнах образуется пена
8 Очень крепкий Трудно идти против ветра
9 Шторм Срывает черепицу
10 Сильный шторм Вырывает деревья с корнем
11 Жестокий шторм Большие разрушения
12 Ураган Опустошительное действие
 |
Особенно широкое распространение реперные шкалы получили в гуманитарных науках, спорте, искусстве и других областях, где измерения еще не достигли высокого совершенства. В спорте чаще всего шкала порядка используется в художественной гимнастике, фигурном катании, единоборствах и т.п. Так, в художественной гимнастике артистизм спортсменок устанавливается в виде рангов: ранг победителя – 1, второе место – 2 и т.д.
Недостатком реперных шкал является неопределенность интервалов между реперными точками. Поэтому баллы нельзя складывать, вычитать, перемножать, делить и т.д. Более совершенным в этом отношении являются шкалы, составленные из строго определенных интервалов. Общепринятым, например, является измерение времени по шкале разбитой на интервалы, равные периоду обращения Земли вокруг Солнца (летоисчисление). Эти интервалы (годы) делятся на более мелкие (сутки), равные периоду обращения Земли вокруг своей оси. Сутки в свою очередь делятся на часы, часы на минуты, минуты на секунды. Такая шкала называется шкалой интервалов (разностей). По шкале интервалов можно уже судить не только о том, что один размер больше другого, но и о том, на сколько больше. Т.е. на шкале интервалов определены такие математические действия, как сложение и вычитание. Данные шкалы интервалов дают ответ на вопрос " на сколько больше? ", но не позволяют утверждать, что одно значение измеренной величины во столько-то раз больше или меньше другого. Например, если: температура повысилась с 10 до 20 по Цельсию, то нельзя сказать, что стало в два раза теплее; в соревнованиях по художественной гимнастике при определении артистичности между второй и четвертой спортсменками два ранга, то это вовсе не означает, что вторая вдвое артистичнее четвертой. Это объясняется тем, что на шкале интервалов известен масштаб, а начало отсчета может быть выбрано произвольно.
Если в качестве одной из двух реперных точек выбрать такую, в которой размер не принимается равным нулю (что приводит к появлению отрицательных значений), а равен нулю на самом деле, то по такой шкале уже можно отсчитывать абсолютное значение размера и определять не только, на сколько один размер больше или меньше другого, но и во сколько раз он больше или меньше. Эта шкала называется шкалой отношений.
Шкала отношений является наиболее совершенной из всех рассматриваемых шкал. Но, к сожалению, построение шкалы отношений возможно не всегда. Время, например, может измеряться только по шкале интервалов. В спорте по шкале отношений измеряют расстояние, силу, скорость и десятки других переменных.
В зависимости от того, на какие интервалы разбита шкала, один и тот же размер представляется по-разному. Например, 0, 001 км; 1 м; 100см; 1000 мм- четыре варианта представления одного и того же размера. Их называют значениями измеряемой величины. Таким образом, значение измеряемой величины - это выражение ее размера в определенных единицах измерения. Входящее в него отвлеченное число называется числовым значением. Оно показывает, на сколько единиц измеряемый размер больше нуля или во сколько раз он больше единицы (измерения). Так, измеряя длину прыжка, мы узнаем, во сколько раз эта длина больше длины другого тела, принятого за единицу длины (метровой линейки в частном случае); взвешивая штангу, определяем отношение ее массы к массе другого тела - единичной гири " килограмма" и т.п.
Самой простой из всех шкал является шкала наименований или номинальная шкала (от латинского слова " номе" - имя). В этой шкале нет отношений типа " больше-меньше". Здесь речь идет о группировке объектов, идентичных по определенному признаку, и о присвоении им обозначений в виде цифр, которые служат для обнаружения и различения изучаемых объектов (например, нумерация игроков в командах). При использовании шкалы наименований могут проводится только некоторые математические операции. Например, можно подсчитывать, сколько раз (как часто) встречается то или иное число.


 Характеристики и примеры шкал измерений
Характеристики и примеры шкал измерений
Шкала Характеристики Математические Примеры
 методы
методы
 Наименований Объекты сгруппированы, Число случаев Номер спортсмена
Наименований Объекты сгруппированы, Число случаев Номер спортсмена
а группы обозначены но- Мода на, амплуа и т.д.
мерами. То, что номер Тетрахорические
одной группы больше или и полихорические
меньше другой, еще ниче- коэффициенты
го не говорит об их свойст- корреляции
вах, за исключением того,
 что они различаются.
что они различаются.
Порядка Числа, присвоенные объек- Медиана Результаты
там, отражают количество Ранговая корреляция ранжирования
свойства, принадлежащего Ранговые критерии спортсменов в тесте
им. Возможно установление Проверка гипотез
соотношения «больше» или непараметрической
«меньше» статистикой

 Интервалов Существует единица изме- Все методы статисти- Температура тела,
Интервалов Существует единица изме- Все методы статисти- Температура тела,
 рений, при помощи которой ки, кроме определения суставные углы
рений, при помощи которой ки, кроме определения суставные углы
объекты можно не только отношений и т.д.
упорядочить, но и приписать
им числа так, чтобы равные
разности отражали разные
различия в количестве из-
меряемого свойства. Нуле-
вая точка произвольна и не
указывает на отсутствие
свойства.
Отношений Числа, присвоенные пред- Все методы статис- Длина и масса тела,
метам, обладают всеми тики сила движений, уско-
свойствами интервальной рение и т.п.
шкалы. На шкале существу-
ет абсолютный нуль, кото-
рый указывает на полное
 отсутствие данного свойства
отсутствие данного свойства

 у объекта. Отношение чисел,
у объекта. Отношение чисел,
присвоенных объектам пос-


 ле измерений, отражают
ле измерений, отражают
количественные отношения

 измеряемого свойства
измеряемого свойства
Основной постулат метрологии.
Любое измерение по шкале отношений предполагает сравнение неизвестного размера с известным и выражение первого через второй в кратном или дольном отношении. В математическом выражении процедура сравнения неизвестного значения с известным и выражения первого через второй в кратном или дольном отношении запишется следующим образом: Q
| Q |
На практике не всегда неизвестный размер может быть представлен для сравнения с единицей. Жидкости и сыпучие вещества, например, предъявляются на взвешивание в таре. Другой пример, когда очень маленькие линейные размеры могут быть измерены только после увеличения их микроскопом или другим прибором. В первом случае процедуру измерения можно выразить отношением – Q+ n, во втором – n Q
| Q | | Q |
где n - масса тары, а n - коэффициент увеличения. Само сравнение, в свою очередь, происходит под влиянием множества случайных и неслучайных, аддитивных (от латинского aditivas - прибавляемый) и мультипликативных (от латинского multiplico - умножаю) факторов, точный учет которых невозможен, а результат совместного воздействия непредсказуем. Если мы ограничимся, для простоты рассмотрения, только аддитивными воздействиями, совместное влияние которых можно учесть случайным слагаемым h, то получим следующее уравнение измерения по шкале отношений: 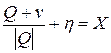
Это уравнение выражает действие, т.е. процедуру сравнения в реальных условиях, которая и является измерением. Отличительной особенностью такой измерительной процедуры является то, что при ее повторении из-за случайного характера h отсчет по шкале отношений Х получается каждый раз разным. Это фундаментальное положение является законом природы. На основании громадного опыта практических измерений сформулировано следующее утверждение, называемое основным постулатом метрологии: отсчет является случайным числом. На этом постулате основана вся метрология.
Полученное уравнение является математической моделью измерения по шкале отношений.
 Аксиомы метрологии. Первая аксиома: без априорной информации измерение невозможно. Эта аксиома метрологии относится к ситуации перед измерением и говорит о том, что если об интересующем нас свойстве мы ничего не знаем, то ничего и не узнаем. С другой стороны, если о нем известно все, то измерение не нужно. Таким образом, измерение обусловлено дефицитом количественной информации о том или ином свойстве объекта или явления и направлено на его уменьшение.
Аксиомы метрологии. Первая аксиома: без априорной информации измерение невозможно. Эта аксиома метрологии относится к ситуации перед измерением и говорит о том, что если об интересующем нас свойстве мы ничего не знаем, то ничего и не узнаем. С другой стороны, если о нем известно все, то измерение не нужно. Таким образом, измерение обусловлено дефицитом количественной информации о том или ином свойстве объекта или явления и направлено на его уменьшение.
Вторая аксиома: измерение есть ни что иное как сравнение. Эта аксиома относится к процедуре измерения и говорит о том, что нет иного экспериментального способа получения информации о каких бы то ни было размерах, кроме как путем сравнения их между собой. Народная мудрость, говорящая о том, что «все познается в сравнении», перекликается здесь с трактовкой измерения Л.Эйлером, данной свыше 200 лет тому назад: «Невозможно определить или измерить одну величину иначе как приняв в качестве известной другую величину этого же рода и указав соотношение, в котором она находится с ней».
Третья аксиома: результат измерения без округления является случайным. Эта аксиома относится к ситуации после измерения и отражает тот факт, что на результат реальной измерительной процедуры всегда оказывает влияние множество разнообразных, в том числе случайных факторов, точный учет которых в принципе невозможен, а окончательный итог непредсказуем. Вследствие этого, как показывает практика, при повторных измерениях одного и того же постоянного размера, либо при одновременном измерении его разными лицами, разными методами и средствами получаются неодинаковые результаты, если только не производить их округления (огрубления). Это отдельные значения случайного по своей природе результата измерения.
Факторы, влияющие на качество измерений.
Получение отсчета (либо принятие решения) – основная измерительная процедура. Однако во внимание должно приниматься еще множество факторов, учет которых представляет иногда довольно сложную задачу. При подготовке и проведении высокоточных измерений в метрологической практике учитывается влияние:
- объекта измерения,
- субъекта (эксперта или экспериментатора),
- способа измерения,
- средства измерения,
- условий измерения.
Объект измерений должен быть достаточно изучен. Перед измерением необходимо представить себе модель исследуемого объекта, которая в дальнейшем, по мере поступления измерительной информации, может изменяться и уточняться. Чем полнее модель соответствует измеряемому объекту или исследуемому явлению, тем точнее измерительный эксперимент.
Для измерений в спорте объект измерений - один из самых сложных моментов, потому что представляет собой переплетение многих взаимосвязанных параметров с большими индивидуальными «разбросами» измеряемых величин (на них в свою очередь, оказывают влияние биологические «внешние» и «внутренние», географические, генетические, психологические, социально-экономические и другие факторы).
Эксперт или экспериментатор вносят в процесс измерения элемент субъективизма, который по возможности должен быть уменьшен. Он зависит от квалификации измерителя, его психофизиологического состояния, соблюдения эргономических требований при измерениях и много другого. Все эти факторы заслуживают внимания. К измерениям допускаются лица, прошедшие специальную подготовку, имеющие соответствующие знания, умения и практические навыки. В ответственных случаях их действия должны быть строго регламентированы.
Влияние средства измерений на измеряемую величину во многих случаях проявляется как возмущающий фактор. Включение электроизмерительных приборов приводит к перераспределению токов и напряжений в электрических цепях и тем самым оказывает влияние на измеряемые величины.
К числу влияющих факторов относятся также условия измерений. Сюда входят температура окружающей среды, влажность, атмосферное давление, электрические и магнитные поля, напряжение в сети питания, тряска, вибрация и многое другое.
Общая характеристика влияющих факторов может быть дана под разными углами зрения: внешние и внутренние, случайные и неслучайные, последние – постоянные и меняющиеся во времени и т.д. и т.п.. Один из вариантов классификации влияющих факторов приведен на рис.1.
 |
1. Качество и количество априорной информации
2. Неадекватность модели объекта
3. Несовершенство метода измерений а-априорные
4. Несовершенство средства измерений
1. 
|
2. Влияние средства измерений на объект
3. Климатические
4. Электрические и магнитные б-в процессе
5. Механические и акустические измерения
6. Ионизирующие излучения и др.
7. Случайные внешние помехи
И внутренние шумы
8. Квалификация и психофизическое
состояние персонала
1.  Качество алгоритма обработки данных
Качество алгоритма обработки данных
2. Несовершенство средств обработки
данных в- апостериорные
3. Квалификация и психофизическое
состояние персонала
Рис.1.Классификация влияющих факторов.
Априорные факторы (а) включают:
1. Влияние на результат измерения качества и количества информации об измеряемом размере. Чем ее больше, чем выше ее качество – тем точнее результат измерения. Накопление априорной информации – один из путей повышения точности результатов измерений.
2. Влияние того очевидного факта, что модель не может в точности соответствовать объекту.
3. Влияние теоретических допущений и упрощений, лежащих в основе метода измерений.
4. Влияние несовершенства измерительного инструмента или прибора, которое может быть как следствием некачественного его изготовления, так и результатом длительной эксплуатации. Отметка шкал показывающих приборов, например, не вполне точно соответствуют измеряемым значениям. В процессе эксплуатации происходит старение материалов, возникает износ механизмов и деталей, развиваются люфты, зазоры, случаются скрытые метрологические отказы (выходы метрологических характеристик за пределы установленных для них норм). Понятно, что результат измерения находится в прямой зависимости от этих факторов.
В процессе измерения (б):
1. Неправильная установка и подготовка к работе средств измерений, принцип действия которых в той или иной степени связан с механическим равновесием, приводит к искажению их показаний. К подобным средствам измерений относятся приборы, в конструкцию которых входит маятник, приборы с подвешенной подвижной частью и др. Многие из них для установки в правильное положение снабжаются уровнями (отвесами, ватерпасами).
2. Влияние средства измерений на объект может до неузнаваемости изменить реальную картину. Например, перераспределение токов и напряжений в электрических цепях при подключении электроизмерительных приборов иногда оказывает заметное влияние на результат измерения.
3. Влияние климатических (температура окружающей среды, относительная влажность воздуха, атмосферное давление), электрических и магнитных (колебания силы электрического тока или напряжения в электрической сети, частоты переменного электрического тока, постоянные и переменные магнитные поля и др.), механических и акустических (вибрации, ударные нагрузки, сотрясения) факторов, а также ионизирующих излучений, газового состава атмосферы и т.п. принято относить к условиям измерений. Такие условия, влиянием которых на результат измерения можно пренебречь, называют нормальными.
1. Случайные внешние помехи и внутренние шумы измерительных приборов оказывают непредсказуемое совместное влияние на результат измерения, вследствие чего он имеет стохастическую природу.
2. Квалификация и психофизическое состояние персонала (или оператора), выполняющего измерение (знания, умения и навыки, сосредоточенность, внимательность, уравновешенность, добросовестность, самочувствие, острота зрения и многое другое), имеют большое значение.
После измерения (в):
1. От правильной обработки экспериментальных данных во многом зависит результат измерения.
2. Технические средства, используемые для обработки экспериментальных данных, не дают новой измерительной информации. Они лишь помогают с большим или меньшим успехом извлекать ее из экспериментальных данных и тем самым оказывают влияние на результат измерения.
3. Неграмотные или безответственные действия персонала (оператора) при обработке экспериментальных данных могут свести на нет любые усилия, затраченные на их получение.
Приведенные классификации далеко не исчерпывают всего многообразия факторов, влияющих на результат измерения.
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1. Что называют измерением?
2. На какие виды делят измерения по способу получения числового значения?
3. Как различаются измерения по характеру изменения измеряемой величины?
4. Какими бывают измерения по количеству измерительной информации?
5. Как делят измерения по отношению к основным единицам?
6. Что такое шкала измерений?
7. Как образуется шкала порядка?
8. Что называется шкалой интервалов?
9. Какие особенности шкалы отношений?
10. Что такое шкала наименований?
11. Как снизить влияние объекта измерений на точность измерительного эксперимента?
12. Как влияют на процесс измерения субъекты измерений?
13. Что можно отнести к условиям измерений?
14. Как снизить влияние объекта измерений на точность измерительного эксперимента?
15. Как влияют на процесс измерения субъекты измерений?
16. Что можно отнести к условиям измерений?
|
|