
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Число обусловленности матрицы системы как мера чувствительности задачи о решении СЛАУ к возмущающим воздействиям
|
|
Определение. Величину
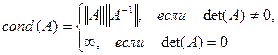 (10)
(10)
называют числом обусловленности матрицы 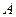 по отношению к используемой матричной норме
по отношению к используемой матричной норме 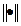 .
.
Для невырожденной матрицы 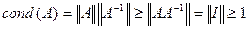 .
.
Определение. Матрица 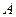 называется хорошо обусловленной, если
называется хорошо обусловленной, если 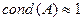 , и плохо обусловленной, если
, и плохо обусловленной, если 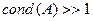 .
.
Замечание. Из (10) вытекает, что значение числа обусловленности матрицы зависит от выбранной для его вычисления матричной нормы, но если матрица 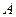 будет хорошо (плохо) обусловленной в какой-либо матричной норме, то она сохранит это свойство и в любой другой матричной норме.
будет хорошо (плохо) обусловленной в какой-либо матричной норме, то она сохранит это свойство и в любой другой матричной норме.
В силу наличия погрешностей при решении СЛАУ, можно считать, что получаемое приближенное решение 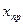 для СЛАУ (5) является точным решением, но некоторой другой – возмущенной – СЛАУ:
для СЛАУ (5) является точным решением, но некоторой другой – возмущенной – СЛАУ:
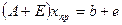 ,
,
где матрица 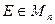 и вектор
и вектор 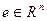 - малые ошибки в начальных данных. можно показать, что относительная погрешность решения СЛАУ (5) может быть оценена выражением:
- малые ошибки в начальных данных. можно показать, что относительная погрешность решения СЛАУ (5) может быть оценена выражением:
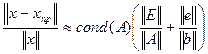 .
.
Таким образом, число обусловленности матрицы системы является мерой чувствительности задачи о решении СЛАУ к погрешностям в начальных данных.
Определение. Пусть 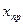 приближенное решения СЛАУ (5), тогда в общем случае
приближенное решения СЛАУ (5), тогда в общем случае 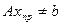 . Назовем вектором невязки вектор
. Назовем вектором невязки вектор 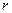 , определяемый в соответствии с формулой:
, определяемый в соответствии с формулой:
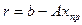 .
.
Вопрос: Если элементы вектора невязки 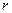 близки к нулю, следует ли из этого, что
близки к нулю, следует ли из этого, что 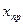 близко к точному решению
близко к точному решению 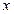 СЛАУ (5)?
СЛАУ (5)?
В общем случае ответ на поставленный вопрос – НЕТ. Покажем это:
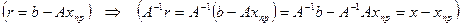 .
.
Поскольку равны векторы 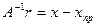 , то равны и их нормы:
, то равны и их нормы:
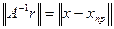 ,
,
тогда
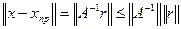 . (15)
. (15)
Из (5) получаем, что
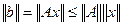 . (20)
. (20)
Перемножим почленно неравенства (15) и (20):
 . (25)
. (25)
Поскольку СЛАУ является неоднородной, то 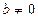 и
и 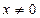 , а следовательно
, а следовательно 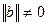 и
и  . Разделим обе части неравенства (25) на
. Разделим обе части неравенства (25) на 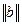
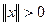 :
:
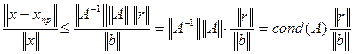 . (30)
. (30)
Из соотношения (30) вытекает, что из «малости» нормы вектора невязки малая относительная погрешность решения СЛАУ следует только тогда, когда матрица СЛАУ является хорошо обусловленной. В противном случае, даже когда  выводов о качестве полученного приближенного решения
выводов о качестве полученного приближенного решения 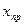 сделать нельзя: за счет большого значения
сделать нельзя: за счет большого значения 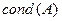
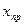 может быть далеко от истинного решения
может быть далеко от истинного решения 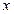 даже при
даже при  .
.
Вопросы
|
|