
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Чувствительность задачи
|
|
Очевидно, что при решении произвольной реальной задачи в общем случае невозможно получить точное значение искомого численного результата. Существование неустранимой погрешности в математической модели объекта или процесса, фигурирующего в задаче, погрешности входных данных, многие из которых в реальных условиях получены экспериментально, погрешность метода, используемого для решения, и вычислительная, погрешности, возникающие при каких-либо дополнительных воздействиях на объект, которые часто трактуются как возмущения входных данных, приводят к необходимости их совокупного учета при оценке погрешности результата. Даже в случае, когда входные данные математической модели не имеют погрешностей, а метод, выбранный для решения полученной математической задачи является точным, избежать вычислительной погрешности при проведении вычислений в системе чисел с плавающей точкой, а значит и погрешности в полученном результате, невозможно. После построения математической модели реального процесса, которая необходимо удовлетворяет требованию адекватности (решение математической задачи, полученное с ее помощью, незначительно отличается от истинного решения реальной задачи), исходная задача и ее математическая формализация в процессе решения и анализа полученного результата, как правило, не разделяются. Однако, в силу особенностей машинной арифметики, невозможно в общем случае получить точное решение даже смоделированной математической задачи (пренебрегая неустранимой погрешностью и погрешностью метода).
Полученное приближенное (в силу перечисленных выше причин) решение некоторой вычислительной задачи  может рассматриваться как точное решение, но другой, возмущенной задачи
может рассматриваться как точное решение, но другой, возмущенной задачи 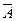 (
(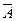 отличается от
отличается от  возмущением входных данных). В этом случае для определения качества полученного приближения необходимо иметь возможность оценить степень зависимости решения от возмущений исходных данных.
возмущением входных данных). В этом случае для определения качества полученного приближения необходимо иметь возможность оценить степень зависимости решения от возмущений исходных данных.
Некоторые вычислительные задачи очень сильно «реагируют» на даже малые изменения данных, причем это не зависит от системы с плавающей точкой или выбранного алгоритма, а является свойством самой задачи.
Пример. Рассмотрим квадратное уравнение, корни которого являются «почти» кратными:
 .
.
Корни уравнения: 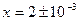 . Изменение правой части уравнения лишь на
. Изменение правой части уравнения лишь на 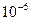 вызовет изменение в корнях
вызовет изменение в корнях 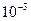 , т.е. на три порядка большее, чем начальное. Рассмотренная задача является чувствительной.
, т.е. на три порядка большее, чем начальное. Рассмотренная задача является чувствительной.
Назовем задачу чувствительной к погрешностям исходных данных, если даже малые погрешности исходных данных могут привести к значительной погрешности результата, и нечувствительной в противном случае.
Для чувствительных задач «правильные» ответы (ответы с очень малой погрешностью) принципиально нельзя получить никаким алгоритмом, поскольку даже малые ошибки, допущенные при представлении данных и при вычислениях (а эти ошибки сопровождают вычислительный процесс всегда) приведут к значительным погрешностям в результатах. В силу этого чрезвычайно важной и актуальной является численная оценка такой чувствительности, установления параметров, определяющих чувствительность, достаточных условий нечувствительности задачи.
Пусть 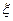 ― входные данные для некоторой задачи, результатом решения которой является
― входные данные для некоторой задачи, результатом решения которой является  ;
; 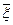 ― возмущенные входные данные, а решение задачи, полученное для этих входных данных, ―
― возмущенные входные данные, а решение задачи, полученное для этих входных данных, ― 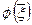 . Числом обусловленности задачи называется величина, определяемая соотношением:
. Числом обусловленности задачи называется величина, определяемая соотношением:
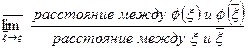 . (2.1)
. (2.1)
Очевидно, чем меньше число обусловленности, тем меньше возмущение результата зависит от возмущения входных данных, тем меньше чувствительность задачи, а при малом числе обусловленности задача окажется нечувствительной к погрешностям исходных данных. Таким образом, число обусловленности задачи является ее мерой чувствительности к возмущающим воздействиям.
Пример. Решить систему уравнений:
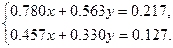
Предположим, что вычисления проводятся в системе с плавающей точкой, для которой  . Решая систему методом Гаусса, получим:
. Решая систему методом Гаусса, получим:
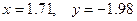 .
.
При подстановке решения в исходную систему получим:
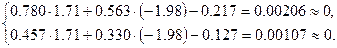
И хотя подстановка показала «хороший результат», точное решение системы, на самом деле, равно:
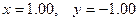 .
.
Вычисленное решение очень отличается от точного, хотя ведет себя примерно также, как точное. Рассмотренная задача является чувствительной (или плохо обусловленной, или некорректно поставленной).
|
|