Оптимизация скорости сходимости метода простой итерации

Лекция 15. Оптимизация скорости сходимости итерационных процессов

План

Возможность обеспечения сходимости метода простой итерации для произвольной матрицы

Процесс симметризации системы

Оптимизация скорости сходимости метода простой итерации

1. Возможность обеспечения сходимости метода простой итерации для произвольной матрицы

Рассматривается СЛАУ

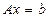, (1)

где 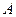- 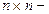матрица системы, 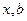- векторы длины неизвестных и правой части соответственно. Проведем ряд эквивалентных преобразований с СЛАУ (1):

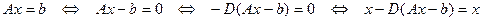, (5)

где 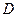- 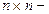матрица. По (5) построим итерационный процесс:

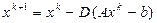. (10)

Преобразуем формулу (10), раскрыв скобки в правой части и вынося за скобки :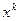

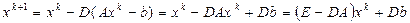, (15)

где 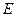- единичная 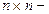матрица. Соотношение (15) отвечает итерационной формуле МПИ: 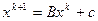(см.лекц.14), в которой матрица 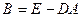, а вектор .

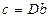Рассмотрим случай, когда 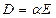, где . Тогда (15) примет вид:

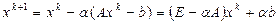. (20)

Сходимость и скорость сходимости итерационного процесса (20) МПИ зависит от величины максимального по модулю собственного значения матрицы 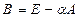(см.лекц.14). Пусть 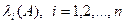, - это собственные значения матрицы 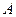, тогда собственные значения матрицы 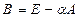будут вычисляться по формуле:

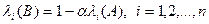, (25)

а собственные векторы матриц 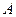и 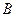будут одинаковыми. Проверим соотношение (25). Пусть 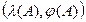- какая-то собственная пара матрицы 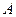. По определению собственной пары это означает, что:

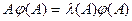(30)

Рассмотрим

(35)

Соотношение (35) подтверждает, что 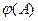является собственным вектором матрицы 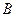, отвечающим собственному значению 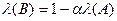. Таким образом, для сходимости итерационного процесса (15), (20) необходимо и достаточно, чтобы

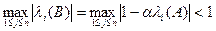. (40)

Для произвольной матрицы 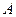ее собственные значения могут быть разных знаков, в этом случае 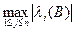, определяемый в соответствии с (40), будет больше 1, и итерационный процесс (15), (20) будет расходиться. Рассмотрим частный случай, когда все . Это соответствует симметричной и положительно определенной матрице. На первый взгляд кажется, что мы значительно сузили область рассматриваемых СЛАУ, однако это не так.

1. Процесс симметризации системы

Любую СЛАУ можно свести к СЛАУ с симметричной и положительно определенной матрицей. Это можно сделать путем умноженя левой и правой частей СЛАУ (1) слева на матрицу :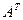

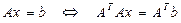. (45)

Процесс (45) называется симметризацией СЛАУ. Полученная система – это СЛАУ с матрицей 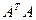. Проверим, что матрица 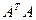является симметричной и положительно определенной. Действительно, из того, что

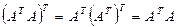
вытекает симметричность 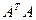. Для доказательства положительной определенности рассмотрим произведение

,

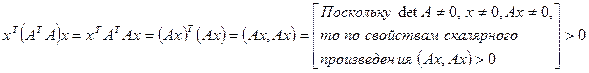что, в силу произвольности ненулевого вектора 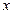, и говорит о положительной определенности матрицы .

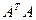После симметризации все собственные значения матрицы 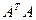СЛАУ положительны, а значит только теперь принципиально возможно говорить о построении сходящегося итерационного процесса (15), (20) для СЛАУ (45), эквивалентной СЛАУ (1).

Замечание. Вычислительная сложность процесса симметризации СЛАУ размера 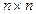, определяемая количеством операций, производимых при умножении двух 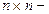матриц, равна 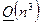. В силу этого, хотя потенциальная возможность приведения любой СЛАУ вида (1) к системе с симметричной и положительно определенной матрицей существует, такой процесс не всегда оказывается желательным.