
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Особенности и преимущества итерационных методов решения систем линейных алгебраических уравнений
|
|
Лекция 14. Особенности и условия применимости итерационных методов решения систем линейных алгебраических уравнений
План
- Особенности и преимущества итерационных методов решения систем линейных алгебраических уравнений
- Метод простой итерации для решения СЛАУ. Условия сходимости метода простой итерации
- Метод Зейделя как модификация метода простой итерации
- Условия сходимости метода Зейделя.
- Метод градиентного спуска
Особенности и преимущества итерационных методов решения систем линейных алгебраических уравнений
Численные методы решения СЛАУ
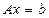 , (1)
, (1)
где 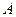 -
- 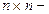 матрица системы,
матрица системы, 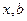 - векторы длины
- векторы длины 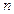 неизвестных и правой части соответственно, как уже отмечалось в лекци 5, делятся на два больших класса: прямые (эти методы в предположении отсутствия округлений дают точное решение СЛАУ после конечного, определяемого заранее числа арифметических операций) и итерационные (точное решение в общем случае получается за бесконечное число шагов).
неизвестных и правой части соответственно, как уже отмечалось в лекци 5, делятся на два больших класса: прямые (эти методы в предположении отсутствия округлений дают точное решение СЛАУ после конечного, определяемого заранее числа арифметических операций) и итерационные (точное решение в общем случае получается за бесконечное число шагов).
В приложениях часто встречаются системы, элементы матриц которых вычисляются по простым формулам или алгоритмам, а потому для решения систем такого рода желательно было бы иметь такие методы, в которых элементы матриц вообще можно было бы не хранить, а генерировать их по мере необходимости. Очевидно, что рассмотренные ранее прямые методы, в частности, различные варианты метода Гаусса, не обладают таким свойством, т.к. в процессе решения элементы матрицы изменяются. Кроме того, в приложениях часто встречаются задачи, в которых матрица СЛАУ имеет слишком большой размер, что для ее хранения не хватает не только оперативной памяти, но и памяти на внешних носителях. Объем вычислений при решении таких систем прямыми методами занимает очень много времени. В этом случае желательно пользоваться такими методами, которые не меняют элементов матрицы. При этом в оперативной памяти хотелось бы хранить лишь несколько строк (или столбцов) матрицы СЛАУ. Всем перечисленным выше пожеланиям удовлетворяют итерационные методы решения СЛАУ.
Как уже отмечалось, общая идея итерационных методов заключается в следующем: по заданной матрице системы 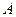 , вектору правой части
, вектору правой части 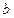 и некоторому начальному приближению
и некоторому начальному приближению 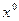 к решению СЛАУ находится следующее приближение
к решению СЛАУ находится следующее приближение 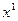 , по которому на следующем шаге строится приближение
, по которому на следующем шаге строится приближение 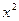 к решению и т.д. Получаем бесконечную векторную последовательность
к решению и т.д. Получаем бесконечную векторную последовательность 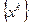 приближений к решению:
приближений к решению: 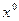 ,
, 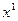 ,...,
,...,  ,.... Итерационный процесс строится таким образом, чтобы
,.... Итерационный процесс строится таким образом, чтобы 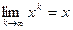 , где
, где 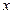 - точное решение СЛАУ.
- точное решение СЛАУ.
Основные особенности итерационных методов:
1. На каждой итерации элементы матрицы СЛАУ 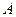 не меняются;
не меняются;
2. Объем вычислений для получения каждого последующего приближения сравним с объемом при умножении матрицы 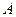 на некоторый вектор. Чаще всего вычисление на каждой итерации и сводится к умножению матрицы на вектор;
на некоторый вектор. Чаще всего вычисление на каждой итерации и сводится к умножению матрицы на вектор;
3. Если известна структура матрицы или известны формулы для вычисления элементов матрицы, то при реализаци вычислений на ЭВМ всю матрицу не обязательно хранить в памяти;
4. Для систем среднего и малого размера, как правило, более предпочтительными являются прямые методы. Итерационные методы применяются, главным образом, для решения задач большого размера.
Особое преимущество итерационных методов перед прямыми ощущается при решении сильно разреженных систем.
|
|