
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Основні поняття, визначення, співвідношення
|
|

 1.1. Сили. Аксіоми статики
1.1. Сили. Аксіоми статики
Сила – це міра механічної дії одного матеріального тіла на інше. Сила євекторною величиною: вона характеризується точкою прикладання, числовим значенням і напрямом.
Точку тіла, на яку діє сила, називають точкою прикладання сили. Пряма, вздовж якої спрямований вектор сили, називають лінією дії сили. Сила, яка прикладена до тіла у точці, називають зосередженою. Сили, що діють на всі точки даної частини поверхні чи об’єму, називають розподіленими.
Дві системи сил називають еквівалентними, якщо, не порушуючи стану твердого тіла, одну з них можна замінити іншою. Силу, яка еквівалентна даній системі сил, називають рівнодійною цієї системи сил. Вираз 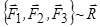 означає, що сила
означає, що сила 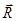 є рівнодійною системи сил
є рівнодійною системи сил 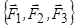 .
.
Система матеріальних точок (або її окремий випадок – тверде тіло) знаходиться у рівновазі відносно нерухомої системи відліку, якщо відносно цієї системи всі її точки знаходяться у стані спокою або рухаються рівномірно й прямолінійно з однаковими за значенням і напрямом швидкостями.
Систему сил називають з рівноваженою, якщо тіло, до якого вона прикладена, знаходиться у рівновазі.
Статика базується на таких аксіомах:
Аксіома 1 (про дві сили). Якщо до твердого тіла прикласти чи відкинути дві рівні за модулем сили, що діють вздовж однієї прямої у протилежних напрямах, то стан тіла не зміниться.
 З цієї аксіоми виходить, що точку прикладання сили можна переносити вздовж лінії дії сили в будь-яку точку тіла, тобто сила є ковзний вектор.
З цієї аксіоми виходить, що точку прикладання сили можна переносити вздовж лінії дії сили в будь-яку точку тіла, тобто сила є ковзний вектор.
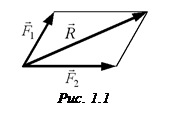
Аксіома 2 (про паралелограм сил). Рівнодійна двох сил, прикладених в одній точці твердого тіла, визначається діагоналлю паралелограма, побудованого на цих силах як на сторонах (рис. 1.1):
 . (1.1)
. (1.1)
Правило додавання сил, що прикладені в одній точці, можна поширити на будь-яку кількість сил:
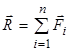 . (1.2)
. (1.2)
Аксіома 3 (про дію та протидію). Сили (дії та протидії), що виникають при взаємодії двох тіл, рівні за модулем, протилежні за напрямом і мають спільну лінію дії.
Зауваження: ці сили прикладені до різних тіл і не утворюють систему сил, еквівалентну нулю (на відміну від двох сил згідно аксіоми 1).
Аксіома 4 (про затвердіння). Рівновага тіла, що може деформуватися, не порушиться, якщо його розглядати як абсолютно тверде тіло.
Зауваження: ця аксіома використовується тоді, коли розглядається рівновага тіла, яке не можна вважати твердим, наприклад, нитка (ланцюг, трос).
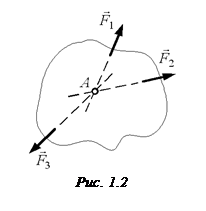 Теорема про три сили. Якщо тіло знаходиться в стані рівноваги під дією трьох непаралельних сил і лінії дії двох сил перетинаються, то всі сили лежать в одній площині і їхні лінії дії перетинаються в одній точці (рис. 1.2).
Теорема про три сили. Якщо тіло знаходиться в стані рівноваги під дією трьох непаралельних сил і лінії дії двох сил перетинаються, то всі сили лежать в одній площині і їхні лінії дії перетинаються в одній точці (рис. 1.2).
Зауваження: цю теорему використовують для визначення лінії дії третьої сили.
Обмеження на рухи твердого тіла, що зберігаються у разі дії на нього будь-яких сил, називаються в’язями твердого тіла.
Дії в’язей на тіло характеризуються силами, які називаються реакціями в’язей (пасивними силами).
Сили поділяють на активні сили та реакції в’язей. До активних сил належать сили, що не зумовлені взаємодією тіла і в’язей.
Найчастіше зустрічаються такі в’язі:
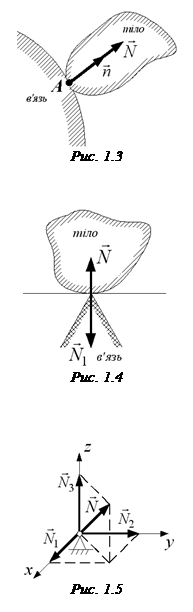 Гладка поверхня (рис. 1.3). Точка дотику А тіла з поверхнею може вільно рухатися вздовж поверхні, але не може рухатися в напрямі, протилежному нормалі
Гладка поверхня (рис. 1.3). Точка дотику А тіла з поверхнею може вільно рухатися вздовж поверхні, але не може рухатися в напрямі, протилежному нормалі 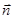 до поверхні. Отже, реакція гладкої поверхні
до поверхні. Отже, реакція гладкої поверхні  спрямована вздовж нормалі
спрямована вздовж нормалі 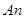 до поверхні (нормаль до поверхні направляємо так, щоб вона виходила з поверхні).
до поверхні (нормаль до поверхні направляємо так, щоб вона виходила з поверхні).
Вістря (рис. 1.4). У цьому випадку поняття нормалі до поверхні в’язі не визначене, тобто реакцію вістря відразу зобразити неможливо. Тому спочатку знай-демо лінію дії реакції  тіла, що діє на вістря, вважаючи, що поверхня тіла є гладкою. Реакція
тіла, що діє на вістря, вважаючи, що поверхня тіла є гладкою. Реакція  напрямлена по нормалі до поверхні тіла. Виходячи з того, що сила
напрямлена по нормалі до поверхні тіла. Виходячи з того, що сила  напрямлена протилежно силі
напрямлена протилежно силі  (сили
(сили  та
та  є силами дії та протидії) отримаємо, що реакція вістря спрямована в бік, протилежний нормалі до поверхні тіла.
є силами дії та протидії) отримаємо, що реакція вістря спрямована в бік, протилежний нормалі до поверхні тіла.
Сферичний шарнір. Умовне зображення наведено на рис. 1.5. Вважається, що поверхня сферич-ного тіла є гладкою, тому реакція шарніра напрямлена по нормалі до поверхні сферичного тіла. Внаслідок сферичності поверхні єдиним, що відомо про реакцію, є те, що вона проходить через центр шарніра, а конкретний напрям реакції невідомий. Тому реакція шарніра зображується або одним вектором  довільного напряму, або трьома складовими:
довільного напряму, або трьома складовими: 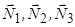 .
.
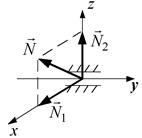
Циліндричний шарнір. На рис. 1.6, а наведено умовне зображення циліндричного шарніра (підп’ятника), що обмежує рух тіла в площині, перпендикулярній до осі шарніра, а також уздовж осі. Реакція може бути зображена або у вигляді одного вектора  довільного напряму, або у вигляді трьох складових
довільного напряму, або у вигляді трьох складових 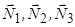 .
.
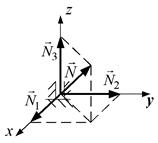 а)
а)
|
 б)
б)
|
| Рис. 1.6 |
На рис. 1.6, б наведено умовне зображення циліндричного шарніра або підшипника, який обмежує рух тільки в площині, перпендикулярній до осі шарніра. Реакція може бути зображена або у вигляді одного вектора  , або у вигляді двох складових
, або у вигляді двох складових  в площині, перпендикулярній до осі шарніра.
в площині, перпендикулярній до осі шарніра.
 Шарнірно – рухома опора (коток) (рис. 1.7). У місці закріп-лення тіла до котка воно не може рухатися тільки в напрямі, про-тилежному нормалі до поверхні, на якій встановлений коток. Отже, реакція котка буде нап-рямлена вздовж нормалі до цієї нерухомої поверхні.
Шарнірно – рухома опора (коток) (рис. 1.7). У місці закріп-лення тіла до котка воно не може рухатися тільки в напрямі, про-тилежному нормалі до поверхні, на якій встановлений коток. Отже, реакція котка буде нап-рямлена вздовж нормалі до цієї нерухомої поверхні.

 Стрижень – тверде тіло, вагою якого нехтують (рис. 1.8), а на кінцях є точкові сферичні шарніри. Щоб визначити напрям реакції в’язі
Стрижень – тверде тіло, вагою якого нехтують (рис. 1.8), а на кінцях є точкові сферичні шарніри. Щоб визначити напрям реакції в’язі  в місці закріплення тіла, спочатку розглянемо сили, що діють на стрижень. На нього діють дві сили:
в місці закріплення тіла, спочатку розглянемо сили, що діють на стрижень. На нього діють дві сили: 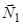 та
та 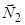 . Згідно аксіоми 1 про дві сили, ці сили мають спільну лінію дії, тобто сили
. Згідно аксіоми 1 про дві сили, ці сили мають спільну лінію дії, тобто сили  напрямлені вздовж лінії, яка з’єднує шарніри. З того, що сили
напрямлені вздовж лінії, яка з’єднує шарніри. З того, що сили 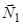 та
та  є силами дії та протидії, виходить, що реакція стрижня також спрямована вздовж прямої, що з’єднує точкові шарніри. Конкретний напрям вектора сили
є силами дії та протидії, виходить, що реакція стрижня також спрямована вздовж прямої, що з’єднує точкові шарніри. Конкретний напрям вектора сили  наперед невідомий, бо стрижень може бути розтягнутим чи стиснутим.
наперед невідомий, бо стрижень може бути розтягнутим чи стиснутим.
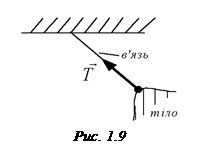 Нитка (її вагою нехтують). Внаслідок того, що нитка заважає тільки в розтягнутому стані руху тіла, її реакція напрямлена в бік, протилежний розтягуванню, як показано на рис. 1.9.
Нитка (її вагою нехтують). Внаслідок того, що нитка заважає тільки в розтягнутому стані руху тіла, її реакція напрямлена в бік, протилежний розтягуванню, як показано на рис. 1.9.
Аксіома про в’язі. Не змінюючи стану твердого тіла, в’язь, накладену на нього, можна відкинути, якщо при цьому прикласти реакцію в’язі у точці взаємодії тіла і в’язі.
Сили поділяють на зовнішні та внутрішні.
Сили, що спричинені дією тіл, які не входять до системи, яка розглядається, називаються з овнішніми.
Сили взаємодії між матеріальними точками чи тілами однієї системи називаються внутрішніми. Поділ сил на зовнішні та внутрішні – умовний. Наприклад, реакція  гладкої поверхні (рис. 1.3) є зовнішньою силою для тіла та внутрішньою для системи поверхня – тіло.
гладкої поверхні (рис. 1.3) є зовнішньою силою для тіла та внутрішньою для системи поверхня – тіло.
Внутрішні сили в твердому тілі зрівноважені згідно
аксіом 1 та 3.
Для визначення внутрішніх сил використовують метод перерізів, згідно якого в тому місці, де треба знайти внутрішню силу, тіло розрізають, внаслідок чого внутрішні сили переводять у зовнішні для кожної з частин тіла.
|
|