
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Постановка задачи. Математическая модель любой ЗЛП имеет вид системы m линейных неравенств и (или) уравнений с n переменными (системы ограничений):
|
|
Математическая модель любой ЗЛП имеет вид системы m линейных неравенств и (или) уравнений с n переменными (системы ограничений):
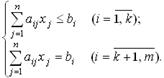
Также задана линейная целевая функция 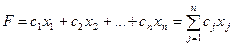 , где cj - целевые коэффициенты.
, где cj - целевые коэффициенты.
Необходимо найти такое решение (множество значений переменных) 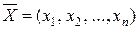 системы ограничений, при котором линейная функция F принимает максимальное (или минимальное) значение:
системы ограничений, при котором линейная функция F принимает максимальное (или минимальное) значение: 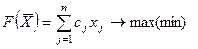 . В общем случае задача может иметь бесконечное множество решений. Решение
. В общем случае задача может иметь бесконечное множество решений. Решение 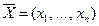 , которое удовлетворяет ограничениям, называют планом. Если все компоненты xj ≥ 0 (
, которое удовлетворяет ограничениям, называют планом. Если все компоненты xj ≥ 0 ( ), то решение (план)
), то решение (план) 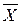 называют допустимым решением (опорным планом). Множество опорных планов образуют область допустимых решений (ОДР).
называют допустимым решением (опорным планом). Множество опорных планов образуют область допустимых решений (ОДР).
Решение  , которое удовлетворяет всем ограничениям, условию неотрицательности всех переменных (xj ≥ 0) и при этом дает max (min) целевой функции F, называется оптимальным решением (оптимальным планом).
, которое удовлетворяет всем ограничениям, условию неотрицательности всех переменных (xj ≥ 0) и при этом дает max (min) целевой функции F, называется оптимальным решением (оптимальным планом).
Условие задачи:
Предприятие планирует выпуск двух видов продукции I и II. На их производство расходуется три вида сырья A, B, C, объемы которых ограничены складскими запасами.
Потребность aij на каждую единицу j -го вида продукции (j = 1, 2) i -го вида сырья (i = 1, 2, 3), запас bi соответствующего вида сырья и прибыль сj от реализации единицы j -го вида продукции (сj – единичная прибыль, целевые коэффициенты) заданы таблицей:
| Виды сырья, i | Виды продукции, j | Запасы сырья, bi | |
| I | II | ||
| ресурсные коэффициенты aij | |||
| A | a 11 = 13 | a 12 = 24 | b 1 = 312 |
| B | a 21 = 32 | a 22 = 32 | b 2 = 480 |
| C | a 31 = 58 | a 32 = 29 | b 3 = 696 |
| Единичная прибыль cj (у. е.) | c 1 = 4 | c 2 = 3 | |
| План (ед.) | x 1 | x 2 |
Из таблицы следует, что для производства единицы изделия I вида требуется затратить 13 кг сырья А, 32 кг сырья В и 58 кг сырья С. Для производства единицы изделия II вида требуется затратить 24 кг сырья А, 32 кг сырья В и 29 кг сырья С. Производство обеспечено запасами сырья А в количестве 312 кг, сырья В – 480 кг, сырья С – 696 кг. Прибыль от реализации единицы готового изделия I вида составит 4 у. е., изделия II вида – 3 у. е.
Заранее планируется произвести продукции обоих видов в количестве не менее 10 единиц.
Требуется составить оптимальный план производства продукции I и II видов 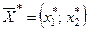 , обеспечивающий максимальную прибыль от ее реализации при условии, что потребление ресурсов по каждому виду продукции не превзойдет имеющихся запасов.
, обеспечивающий максимальную прибыль от ее реализации при условии, что потребление ресурсов по каждому виду продукции не превзойдет имеющихся запасов.
Обозначим через неизвестную x 1 – количество изделий I вида, x 2 – количество изделий II вида, которое необходимо производить.
В условии задачи сформулированы ограничения на запасы каждого вида сырья, т.е. потребление ресурсов по каждому виду (А, В, С) не превзойдет имеющихся запасов bi. Кроме того, ограничения накладываются на общее количество производимой продукции (не менее 10 ед.), а также необходимо указать неотрицательность переменных x 1≥ 0, x 2≥ 0.
Запишем эти ограничения в виде системы неравенств (составляем математическую модель):
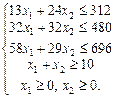 (1)
(1)
Например, величина 13 х 1 в первом неравенстве – это количество сырья А, необходимое для производства продукции I вида в количестве х 1 изделий. Четвертое неравенство (x 1 + x 2 ≥ 10) представляет собой условие на ограничение производимого количества продукции обоих видов.
Составим целевую функцию общей прибыли, получаемой от реализации всей произведенной продукции:  . Здесь 4 х 1 – прибыль от продажи х 1 единиц продукции I вида, 3 х 2 – прибыль от продажи х 2 единиц продукции II вида.
. Здесь 4 х 1 – прибыль от продажи х 1 единиц продукции I вида, 3 х 2 – прибыль от продажи х 2 единиц продукции II вида.
|
|