
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Свойства куба
|
|
1. У куба все грани — квадраты.
2. a√ 3 (d² = a² + a² + a², где a — ребро куба, d — диагональ куба).
3. Vкуба = a³.
4. Sбок. куба = 4a²; Sполн. куба = 6a2
Задача 1.Боковое ребро наклонной призмы равно 15 см и наклонено к плоскости основания под углом 30о. Найдите высоту призмы (рис.48)
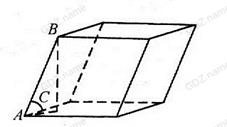
Рис.48
ВО - перпендикуляр в основанию, так что ∆ АВО - прямоугольный.
Значит ВС=АВ∙ sinВАС =1, 5∙ sin 30o =7, 5 (см)
Ответ: 7, 5 см.
Задача 2. В прямой треугольной призме все ребра равны. Боковая поверхность равна
12 м2. Найти высоту.
Решение:
Так как все ребра равны, то боковые грани являются квадратами. Площадь одной грани равна трети площади боковой поверхности: 12: 3 = 4 (м2). Значит, сторона квадрата равна 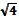 = 2 (м). Тогда ребро призмы равно высоте и равно 2м.
= 2 (м). Тогда ребро призмы равно высоте и равно 2м.
Ответ: 2 м.
Задача 3. Боковая поверхность правильной четырехугольной призмы равна 32 м2, а полная поверхность равна 40 м2. Найти высоту.
Решение:
Так как площадь поверхности S = Sбок + 2Sосн, то площадь поверхности основания равна Sосн = (40 – 32): 2 = 4 (м2).
В основании находится квадрат, так как призма правильная, так что сторона квадрата равна 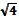 = 2 (м).
= 2 (м).
Боковая поверхность правильной призмы равна: Sбок = р∙ h = 4 а∙ h, так что
h = S: (4 а) = 32: (4 ∙ 2) = 4 (м2)
Ответ: 4 м.
Задача 4. В правильной четырехугольной призме площадь основания равны 144 см2, а высота рана 14см. Определить диагональ этой призмы.
Решение:
Так как призма правильная, то в основании ее лежит квадрат и его площадь равна: S=a2
Тогда a= 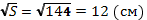
Далее, заметим, что правильная четырехугольная призма является прямоугольным параллелепипедом, так что квадрат любой диагонали равен сумме квадратов трех его измерений, так что:
d 2=a2+a2+h2= 122+122+142=484, d = 22(см)
Задачи
Цель. Учиться изображать основные многогранники, выполнять чертежи по условиям задач; решать планиметрические и простейшие стереометрические задачи на нахождение геометрических величин (длин, углов), использовать при решении стереометрических задач планиметрические факты и методы.
 |
1. Боковое ребро прямого параллелепипеда равно 5м, стороны основания равны 6м и 8м, одна из диагоналей основания равна 12м. Определить диагонали параллелепипеда.
2. В прямом параллелепипеде стороны основания 3см и 5см, одна из диагоналей основания 4 см. Меньшая диагональ параллелепипеда с плоскостью основания составляет угол в 60о. определить диагонали параллелепипеда.
3. Поверхность куба равна 24 м2. Найти его ребро
4. Определить поверхность прямоугольного параллелепипеда по трем его измерениям: 10 см, 22см, 16 см.
5. В прямом параллелепипеде стороны основания равны 6 м и 8м и образуют угол в 30о; боковое ребро равно 5 м. Определить полную поверхность этого параллелепипеда.
 |
6. Определить полную поверхность прямой треугольной призмы, если ее высота равна 50 см, а стороны основания 40 см, 13 см, 37 см.
7. В прямой треугольной призме стороны основания равны 25 дм, 29 дм и 36 дм, а полная поверхность содержит 1620 дм2. Определить боковую поверхность призмы.
8. Расстояние между боковыми ребрами наклонной треугольной призмы: 2 см, 3см, 4 см. Боковая поверхность равна 45см2. Найти боковое ребро.
Ответы к задачам
1.13 м и 10 м. 2. 8 см и 10 см. 3. 2м. 4. 1464 см2. 5. 188 м2 . 6. 4980 дм2. 7. 9м2
|
|