Формулировка деформаций

Лекция 4

Математические модели материалов

Конструкционные материалы обладают тремя основными механическими свойствами: упругостью, пластичностью и вязкостью. Эти свойства проявляются в разной степени в зависимости от структуры материала, условий эксплуатации (температура, влажность и т. п.) и типа нагрузки (статической, динамической, импульсной или длительной и т. п.). При различных комбинациях этих факторов один и тот же материал может проявлять одно из механических свойств или некоторую их комбинацию. При изменении некоторых из названных факторов можно изменить поведение материала и получить другую преобладающую комбинацию механических свойств. Теоретическое описание поведения материала производится при помощи механико-математических моделей, которые описывают реальное поведение материала, отражая его наиболее характерные свойства.

Настоящая лекция посвящена в первую очередь нелинейным моделям материалов. Основные соотношения для линейного поведения материала рассмотрены в Лекции 2.

Нелинейность в поведении материалов возникает в связи с тем, что деформации и напряжения связаны нелинейно, т.е. напряжения являются нелинейной функцией деформаций. Часто напряжения зависят (нелинейно) не только от текущего значения деформаций, но и от истории деформирования.

К пакетах конечно-элементного моделирования какие-то модели материалов могут применяться только вместе со специальными элементами (например, модель бетона или вязкоупругая модель), а часть элементов может допускать использование для них различных математических моделей материалов.

Важно отметить, что в моделях материалов для различных конечных элементов может использоваться различное число компонентов напряжений и деформаций. Один компонент X, четыре компонента X, Y, Z, XY или шесть компонентов X, Y, Z, XY, YZ, XZ.

Формулировка деформаций

Для нелинейных материалов упругие деформации определяются следующим способом:

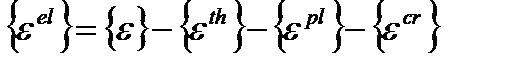, (4.1)

где { ε ^el } – вектор упругих деформаций;

{ ε } – вектор полных деформаций;

{ ε ^th } – вектор температурных деформаций;

{ ε ^pl } – вектор пластических деформаций;

{ ε ^cr } – вектор деформаций ползучести.

В данном случае под вектором полных деформаций { ε } мы понимаем деформации, которые покажет нам тензометрический датчик.

Существует и используется в пакетах конечно-элементного моделирования и другая формулировка полных деформаций:

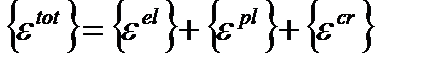. (4.2)

Очевидно, что

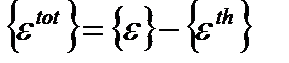. (4.3)

Разница между двумя определениями «полных» деформаций возникла в связи с разным их использованием: { ε } применяется для сравнений с показаниями тензометрических датчиков, а { ε ^tot } для построения кривых, описывающих поведение материала.

Выражение (4.1) может быть дополнено компонентами каких-то особых (уникальных) деформаций, которые в настоящей лекции не рассматриваются.