Теорема 1 (перше правило).

Нехай функція 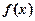неперервна на деякому інтервалі, в якому міститься критична точка х ₀, і диференційовна в усіх точках цього інтервалу (крім, можливо, самої точки х ₀). Якщо при переході зліва направо через цю точку похідна:

1) змінює знак з «+» на «–», то при х = х ₀ функція має максимум;

2) змінює знак «–» на «+», то функція має у цій точці мінімум;

3) не змінює свого знака, то функція в точці х = х ₀ екстремуму не має.

Геометрична ілюстрація теореми 1 (рис. 5). Нехай у точці х = х ₁ маємо 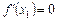і для всіх х, достатньо близьких до точки х ₁, виконуються нерівності

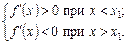
Рис. 5

Тоді при 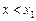дотична до кривої утворює з віссю Ох гострий кут — функція зростає, а при 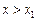дотична утворює з віссю Ох тупий кут — функція спадає; при х = х ₁ функція переходить від зростання до спадання, тобто має максимум.

Якщо в точці х ₂ маємо і для всіх значень х, достатньо близьких до точки х ₂, виконуються нерівності

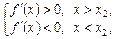
то при 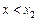дотична до кривої утворює з віссю Ох тупий кут — функція спадає, а при 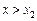дотична до кривої утворює гострий кут — функція зростає. При х = х ₂ функція переходить від спадання до зростання, тобто має мінімум.

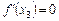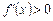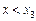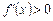Якщо при х = х ₃ маємо і для всіх значень х, достатньо близьких до х ₃, виконуються нерівності при ; при 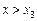, то функція зростає як при 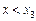, так і при 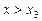. Звідси при х = х ₃ функція не має ні максимуму, ні мінімуму.

Зауваження. На основі даної теореми можна сформулювати таке правило для дослідження неперервної функції 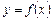на максимум і мінімум.

1. Знаходимо першу похідну функції, тобто .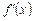

2. Обчислюємо критичні значення аргументу х (критичні точки), для цього:

а) прирівнюємо першу похідну до нуля і знаходимо дійсні корені здобутого рівняння ;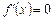

б) знаходимо значення х, для яких похідна 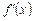має розрив.

3. Досліджуємо знак похідної ліворуч і праворуч від критичної точки. Оскільки знак похідної залишається сталим в інтервалі між двома критичними точками, для дослідження знака похідної ліворуч і праворуч, наприклад від критичної точки х ₂, досить визначити знак похідної в точках 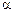і 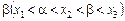, де х ₁ і х ₃ — найближчі критичні точки).

4. Обчислюємо значення функції 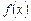у кожній критичній точці.

Таким чином, маємо таке схематичне зображення можливих випадків:

Теорема 2 (друге правило). Якщо для диференційовної функції у деякій точці х ₀ її перша похідна 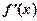дорівнює нулю, а друга похідна 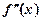існує й відмінна від нуля, тоб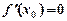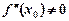то , , то:

1) якщо друга похідна 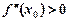, то в точці х ₀ функція 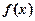має мінімум;

2) якщо 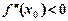— максимум;

3) якщо 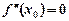— питання залишається відкритим, і для його розв’язання треба застосувати перше правило.

Зауваження. Для критичних точок, в яких похідна функції не існує або дорівнює нескінченності, друге правило не застосовується.

6. Найбільше і найменше значення функції на відрізку

Якщо функція 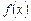неперервна на проміжку [ a; b ], то вона набуває на цьому проміжку свого найбільшого й найменшого значення.

Найбільше значення функції на проміжку [ a; b ] називається абсолютним максимумом, а найменше — абсолютним мінімумом.

Припустимо, що на даному проміжку функція 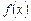має скінченне число критичних точок. Якщо найбільше значення досягається в середині проміжку [ a; b ], то очевидно, що це значення буде одним із максимумів функції (якщо існує кілька максимумів), точніше — найбільшим максимумом. Однак можливо, що найбільше значення досягатиметься на одному з кінців проміжку.

На підставі результатів дослідження будуємо графік функції. Для точнішої побудови візьмемо додатково точки на рис. 6: (–5; – 0, 3), 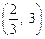, (2; 3), (3; 1, 3).

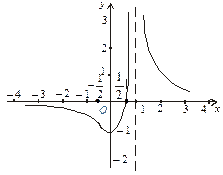
Рис.6