
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Симплекс метод в общем виде
|
|
Требуется найти максимум целевой функции:
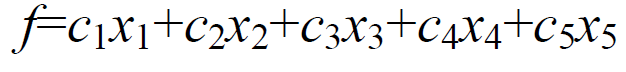 (1)
(1)
При ограничениях:
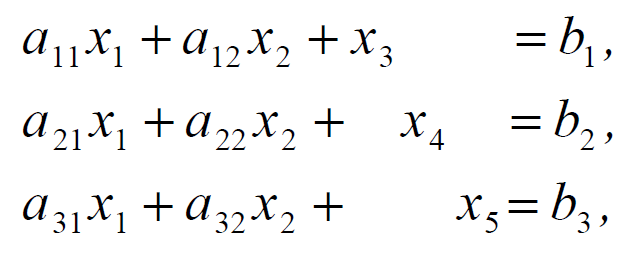 (2)
(2)
И условиях неотрицательности:
xi ≥ 0, i=1, 2,..., n (3)
Из системы (2) видно, что если за свободные неизвестные принять х1, х2 и положить их равными нулю, то базисные неизвестные х3, х4, х5 будут равны правым частям системы. в результате получаем план:
х1=0, х2=0, х3=b1, x4=b2, x5=b3 (4)
Для которого целевая функция равна
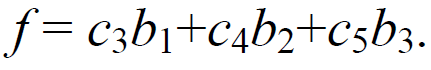 (5)
(5)
Выразим из (2) базисные неизвестные х3, х4, х5 через свободные х1, х2:
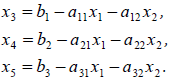 (6)
(6)
Подставим (6) в целевую функцию (1) и после приведения подобных членов будем иметь:
f = (c 1– c 3 a 11– c 4 a 21– c 5 a 31) x 1 + (c 2– c 3 a 12– c 4 a 22– c 5 a 32) x 2 + c 3 b 1 + c 4 b 2 + c 5 b 3. (7)
Если коэффициенты перед х1, х2 в (7) окажутся отрицательными, то целевую функцию нельзя увеличить, переводя эти свободные неизвестные в базисные, то есть давая им какие-то положительное значения. Отрицательность коэффициентов перед неизвестными в (7) есть признак того, что найдено оптимальное решение. Коэффициенты перед свободными неизвестными в выражении для целевой функции принято называть оценками. Введем обозначения:
Z 1 = c 3 a 11 + c 4 a 21 + c 5 a 31, Z 2 = c 3 a 12 + c 4 a 22 + c 5 a 32. (8)
В этих обозначениях условия максимальности запишутся:
c 1 – Z 1 < 0, c 2 – Z 2 < 0, (9)
Пусть условии оптимальности (9) не выполнены, а именно пусть, для определенности, коэффициент перед х1 в (7) положителен, тогда, увеличивая х1, мы увеличим целевую функцию по сравнению с ее значением (5). Посмотрим, насколько может быть увеличена переменная х1по сравнению с нулем, при условии, что х2 остается свободной, то есть будет иметь неизменное значение х2=0. Из (6) видно, что увеличение х1 будет вести к уменьшению х3, х4, х5, если коэффициенты перед х1 в (6) отрицательны. Увеличивать х1 можно лишь до значения, при котором первая из неизвестных х3, х4, х5 обратится в нуль. Положив нулю левые части (6), получим три уравнения:
0 = b 1 – a 11 x 1, 0 = b 2 – a 21 x 1, 0 = b 3 – a 31 x 1.
Если положить:
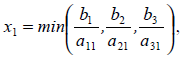 (10)
(10)
то только одна неизвестная из х3, х4, х5 обратится в нуль, то есть станет свободной, а остальные останутся положительными. Предположим, что это будет х3, тогда будем иметь в качестве свободных неизвестных х2, х3 и в качестве базисных х1, х4, х5.
Для удобства дальнейших вычислений желательно преобразовать систему ограничений к виду (2), который характерен тем, что столбцы коэффициентов при базисных неизвестных образуют единичную матрицу. Так как старая базисная переменная х3 заменяется новой базисной переменной х1, то в первом уравнении коэффициент перед х1 должен быть равен 1. Это достигается делением первого уравнения на a11. Далее следует исключить неизвестную х1 из второго и третьего уравнений. Для этого преобразованное первое уравнение умножим сначала на а21 и вычтем из второго, затем на а31 и вычтем из третьего. В результате этих преобразований система (2) примет вид:
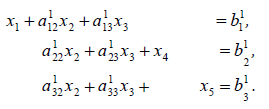 (11)
(11)
Здесь через a1ij обозначены новые значения коэффициентов. Заметим, что подобные преобразования выполняются в методе Гаусса при решении систем линейных уравнений.
Описание выше действия по работе с системой ограничений (2) следует повторить для системы (11) и т.д., до тех пор, пока не будет выполнены условия оптимальности.
Для удобства и компактности вычислений по симлекс-методу применяются симплексные таблицы.
|
|