Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Метод вариации постоянных для решения неоднородных дифференциальных уравнений высших порядков.

Данные уравнения имеют вид

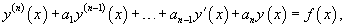
где a1, a2,..., an − действительные или комплексные числа, а правая часть f(x) является непрерывной функцией на некотором отрезке [a, b].

Используя линейный дифференциальный оператор L(D), равный

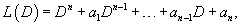
неоднородное дифференциальное уравнение можно записать в виде

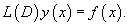
Общее решение y(x) неоднородного уравнения представляется в виде суммы общего решения y0(x) соответствующего однородного уравнения и частного решения y1(x) неоднородного уравнения:

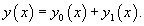
При произвольной правой части f(x) для поиска общего решения неоднородного уравнения используется метод вариации постоянных. В случае, если правая часть представляет собой произведение многочлена и экспоненциальной функции, частное решение удобнее искать методом неопределенных коэффициентов.

Метод вариации постоянных

Предположим, что общее решение однородного дифференциального уравнения n-го порядка известно и представляется формулой

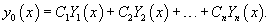
Метод вариации постоянных (или метод Лагранжа) заключается в том, что вместо постоянных чисел C1, C2,..., Cn мы рассматриваем функции C1(x), C2(x),..., Cn(x). Эти функции подбираются таким образом, чтобы решение

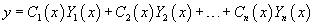
удовлетворяло исходному неоднородному уравнению.

Производные n неизвестных функций C1(x), C2(x),..., Cn(x) определяются из системы n уравнений:

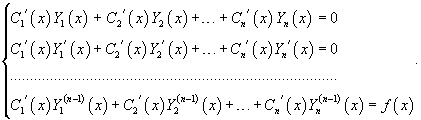
Определителем этой системы является вронскиан функций Y1, Y2,..., Yn, образующих фундаментальную систему решений. В силу линейной независимости этих функций определитель не равен нулю и данная система однозначно разрешима. Окончательные выражения для функций C1(x), C2(x),..., Cn(x) находятся в результате интегрирования.

Найти общее решение дифференциального уравнения y''' + 3y'' − 10y' = x − 3.

Решение.

Сначала найдем общее решение однородного уравнения

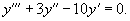
Вычислим корни характеристического уравнения:

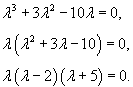
Следовательно,

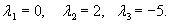
Общее решение однородного уравнения имеет вид:

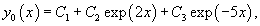
где C1, C2, C3 − произвольные числа.

В правой части уравнения содержится лишь многочлен. Однако, если учесть, что exp(0) = 1, то видно, что на самом деле мы имеем резонансный случай (в замаскированном виде), поскольку один из корней характеристического уравнения также равен нулю: λ 1 = 0. Поэтому частное решение будем искать в виде

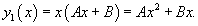
Подставляем производные

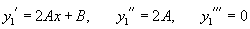
в неоднородное уравнение и определяем коэффициенты A, B:

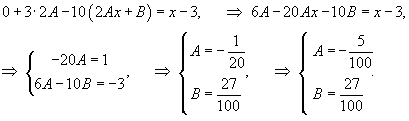
Частное решение y1 записывается как

Итак, общее решение неоднородного дифференциального уравнения выражается формулой