
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Числовые ряды. Сходимость и сумма ряда. Свойства сходящихся рядов. Необходимый признак сходимости.
|
|
Числовой ряд – это сумма членов числовой последовательности вида 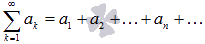 .Суммой сходящегося числового ряда
.Суммой сходящегося числового ряда 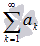 называется предел последовательности его частичных сумм, то есть,
называется предел последовательности его частичных сумм, то есть, 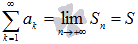 .
.
Свойства сходящихся числовых рядов.
Если сходится числовой ряд 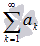 , то сходящимся будет и ряд
, то сходящимся будет и ряд 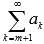 . Другими словами, сходящимся будет и ряд без первых m членов. Если к сходящемуся числовому ряду
. Другими словами, сходящимся будет и ряд без первых m членов. Если к сходящемуся числовому ряду 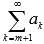 добавить несколько членов (от первого до m-ого), то полученный ряд также будет сходящимся.
добавить несколько членов (от первого до m-ого), то полученный ряд также будет сходящимся.
Если сходится числовой ряд 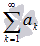 и его сумма равна S, то сходящимся будет и ряд
и его сумма равна S, то сходящимся будет и ряд 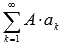 , причем
, причем 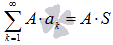 , где A – произвольная постоянная.
, где A – произвольная постоянная.
Если сходятся числовые ряды 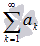 и
и 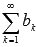 , их суммы равны A и B соответственно, то сходящимися будут ряды
, их суммы равны A и B соответственно, то сходящимися будут ряды 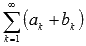 и
и  , причем их суммы будут равны A + B и A - B соответственно.
, причем их суммы будут равны A + B и A - B соответственно.
| Необходимый признак сходимости ряда |
Теорема. Если ряд сходится, то 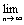 un=0.
Доказательство. Пусть ряд u1+u2+…+un… сходится, то есть существует конечный предел un=0.
Доказательство. Пусть ряд u1+u2+…+un… сходится, то есть существует конечный предел  =S. Тогда имеет место также равенство =S. Тогда имеет место также равенство 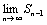 =S, так как при n =S, так как при n 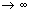 и (n-1) и (n-1) 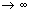 . Вычитая почленно из первого равенства второе, получаем . Вычитая почленно из первого равенства второе, получаем  - - 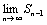 = = 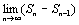 = = 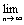 un=0, что и требовалось доказать.
Следствие. Если un=0, что и требовалось доказать.
Следствие. Если 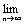 un≠ 0, то ряд u1+u2+…+un… расходится. un≠ 0, то ряд u1+u2+…+un… расходится.
|
|
|