Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Для новых пользователей первый месяц бесплатно. Чат-бот для мастеров и специалистов, который упрощает ведение записей: — Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать; Начать пользоваться сервисом
Методические указания. Передаточная функция системы W(s) – это отношение изображения по Лапласу сигнала на выходе к изображению по Лапласу сигнала на входе при нулевых начальных
|
|
Передаточная функция системы W (s) – это отношение изображения по Лапласу сигнала на выходе к изображению по Лапласу сигнала на входе при нулевых начальных условиях.
Чтобы перейти от передаточной функции к дифференциальному уравнению системы, нужно перейти из области изображений по Лапласу во временную область. Из (1) следует
;
.
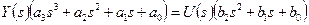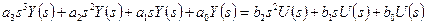Для перехода во временную область воспользуемся формальными правилами:
.
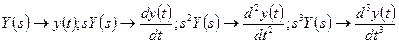Тогда дифференциальное уравнение системы имеет вид:
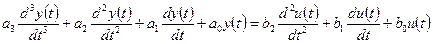. (2)
Характеристическое уравнение системы определяется знаменателем передаточной функции:
.
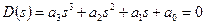Корни данного многочлена (нелинейного уравнения) 
, 
, 
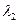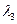можно определить следующими методами:
- методом половинного деления;
- методом Ньютона;
- методом секущих;
- методом простых итераций.
Далее передаточная функция системы записывается в форме нулей и полюсов. Затем разлагаем передаточную функцию на сумму простых слагаемых, используем метод неопределенных коэффициентов.
Полученную СЛАУ решаем одним из следующих методов:
- методом Гаусса;
- методом простых итераций.
В итоге записываем передаточную функцию с учетом найденных коэффициентов.
Импульсная переходная характеристика w (t) – это процесс изменения сигнала на выходе при подаче на вход δ - функции. Ее можно найти в результате обратного преобразования Лапласа, примененного к каждому слагаемому передаточной функции.
В соответствии с таблицами соответствия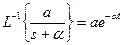 
. Проведем преобразование 
.
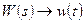Переходная характеристика h (t) – это процесс изменения сигнала на выходе системы при подаче на вход единичного ступенчатого воздействия. Преобразование по Лапласу l(t) это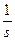 
, следовательно, 
.
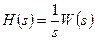Переходную характеристику можно также вычислить следующим образом:
.
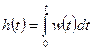Данный интеграл вычисляется одним из следующих методов:
- методом трапеций;
- методом Симпсона.
Построение асимптотических ЛАХ и ФЧХ.При определении частотных характеристик подразумевается, что на входе и выходе системы сигналы являются гармоническими.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Амплитудно-частотная характеристика (АЧХ) показывает, как изменяется отношение выходного сигнала к входному в зависимости от частоты. Фазочастотная характеристика (ФЧХ) показывает изменение сдвига фаз между входным и выходным сигналами в зависимости от частоты.
ЛАЧХ строится в двойных логарифмических шкалах. По одной логарифмической оси откладывается круговая частота w, по другой значение L (w) = 20lg K, выраженное в децибелах. Асимптотическая ЛАЧХ состоит из отрезков прямых линий с наклонами кратными 20 дБ/дек.
Кроме входных и выходных переменных при описании систем выделяют переменные x, связанные с внутренней структурой устройства, – переменные состояния. Тогда систему можно описать с помощью уравнений состояния.
Нормальная форма уравнений состояния имеет вид:
. (3)
Здесь А – квадратная матрица определенного вида, размер которой определяется порядком дифференциального уравнения. Элементы, стоящие над главной диагональю – единицы, элементы нижней строки – коэффициенты левой части дифференциального уравнения, взятые с противоположным знаком. Все остальные элементы – нули. Такая матрица называется матрицей Фробениуса:
.
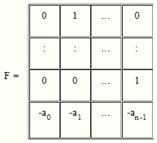Элементы матриц B и D вычисляются по рекуррентным соотношениям.
Подставив в (3) рассчитанные матрицы, получим систему дифференциальных уравнений 1-го порядка.
На основе полученной системы строим схему модели, например:
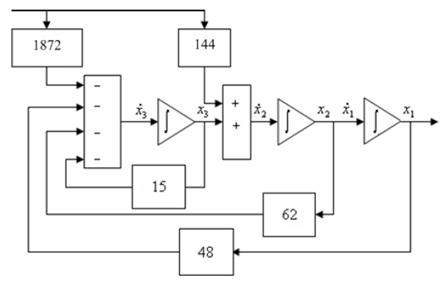
Запишем уравнения состояния в канонической форме. Для этого введем новую переменную состояния q, которая связана с переменной состояния x следующим образом: х = М q. М – это модальная матрица, которая имеет вид:
,
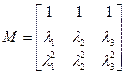где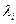 
- характеристические числа матрицы Фробениуса.
При подстановке q вместо x в нормальную форму уравнений состояния (3) получим уравнения состояния системы в канонической форме:
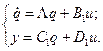
Здесь:
;
;
;
.
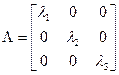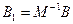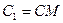Подставив найденные значения матриц в (4), получим систему дифференциальных уравнений 1-го порядка относительно q.
На основе полученной системы строим схему модели, например:
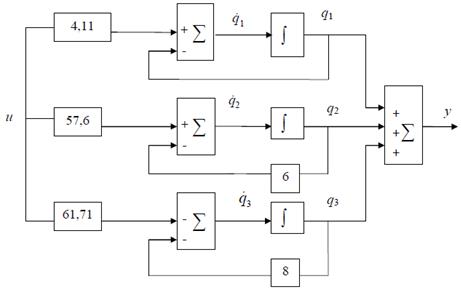
Найдем решение y (t) для системы уравнений в нормальной форме, если заданы начальные условия.
Решение уравнения состояния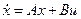 
складывается из двух составляющих x (t) = x 1(t) + x 2 (t) – свободной и вынужденной.
Свободная составляющая x1 (t) – это общее решение дифференциального уравнения системы с нулевой правой частью. Оно не зависит от внешнего воздействия и характеризует естественное поведение системы.
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
Вынужденная составляющая x 2(t) – это частное решение дифференциального уравнения с ненулевой правой частью. Оно зависит от сигнала u (t) и характеризует поведение системы под его воздействием.
Решение уравнения состояния 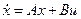имеет вид:
,
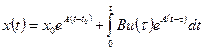где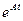 
- фундаментальная матрица или матрица перехода.
Она вычисляется по следующей формуле:
,
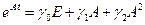где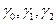 
- неизвестные коэффициенты.
Вычислить их можно, решая матричное уравнение:
.
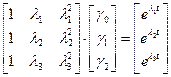Найдем решение уравнений состояния, представленных в канонической форме (4). Каждое из дифференциальных уравнений первого порядка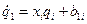 
зависит только от одной переменной, и его решение в общем виде имеет вид:
.
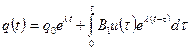Проверяем решение нормальных и канонических уравнений.
Проверим, одинаково ли значение коэффициента усиления: по передаточной функции, переходной характеристике, моделям в пространстве состояний, аналитической записи импульсной переходной характеристики.
После проверки делаем соответствующие выводы.
|
|