Устойчивость сжатых стержней. Продольный изгиб

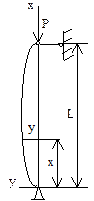Разрушение стержня может произойти не только потому, что будет нарушена прочность, но и оттого, что стержень не сохранит заданной формы. Например, изгиб при продольном сжатии тонкой линейки. Потеря устойчивости прямолинейной формы равновесия центрально сжатого стержня называется продольным изгибом. Упругое равновесие устойчиво, если деформированное тело при любом малом отклонении от состояния равновесия стремится вернуться к первоначальному состоянию и возвращается к нему при удалении внешнего воздействия. Нагрузка, превышение которой вызывает потерю устойчивости, называется критической нагрузкой Р_кр (критической силой). Допускаема нагрузка [P]=P_кр/n_у, n_у – нормативный коэффициент запаса устойчивости. Приближенное дифференциальное ур-ние упругой линии: 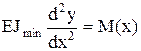, Е –модуль упругости материала стержня, М – изгибающий момент, J_min– наименьший момент инерции сечения стержня. При потере устойчивости прогиб, как правило, происходит перпендикулярно к оси наименьшей жесткости, относительно которой — J=J_min. Рассматривается приближенное дифф-ное ур-ие, т.к. потеря устойчивости возникает при малых деформациях. M=—Py, получаем однородное дифф-ное уравнени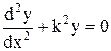е: , где 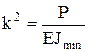. Решая дифф-ное ур-ие находим наименьшее значение критической силы – формула Эйлера: 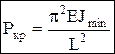– формула дает значение критической силы для стержня с шарнирно закрепленными концами. При различных закреплениях: 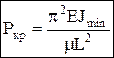, m – коэффициент приведения длины.

При шарнирном закреплении обоих концов стержня m=1; для стержня с заделанными концами m=0, 5; для стержня с одним заделанным и другим свободным концом m=2; для стержня с одним заделанным и другим шарнирно закрепленным концом m=0, 7.

Критическое сжимающее напр-ние.: 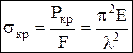, 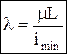– гибкость стержня, 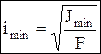– наименьший главный радиус инерции площади сечения стержня. Эти формулы справедливы только тогда, когда напряжения s_кр£ s_пц– предел пропорциональности, т.е. в пределах применимости закона Гука. Формула Эйлера применима при гибкости стержня: 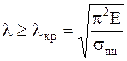, например, для стали Ст3 (С235) l_кр»100. Для случая l< l_кр критическое напряжение вычисляется по эмпирической (полученной экспериментально) формуле Ясинского: s_кр= a — b× l, коэффициенты " a" и " b" в справочной лит-ре (Ст3: a=310МПа; b=1, 14МПа).

Достаточно короткие стержни, для которых l< l₀=40 (для сталей) назыв-тся стержни малой гибкости. Такие стержни рассчитывают только на прочность, т.е. принимают s_кр=s_т (предел текучести) – для пластичных материалов и s_кр=s_В (временное сопротивление) – для хрупких материалов. При расчете стержней большой гибкости используют условие устойчивости: 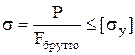, F_брутто– полная площадь сечения,

(F_нетто=F_брутто—F_ослабл –площадь ослабленного сечения с учетом площади отверстий в сечении F_ослабл, например, от заклепок). [s_у]=s_кр/n_у, n_у– нормативный коэф. запаса устойчивости. Допускаемое напряжение [s_у] выражается через основное допускаемое напряжение [s], используемое при расчетах на прочность: [s_у]=j× [s], j – коэффициент уменьшения допускаемого напряжения для сжатых стержней (коэффициент продольного изгиба). Значения j приведены в табл. в учебниках и зависят от материала стержня и его гибкости (например, для стали Ст3 при l=120 j=0, 45).

При проектировочном расчете требуемой площади сечения на первом шаге принимают j₁=0, 5–0, 6; находят: 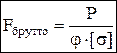. Далее зная F_брутто, подбирают сечение, определяют J_min, i_min и l, устанавливают по табл. фактическое j₁^I, если оно существенно отличается от j₁, расчет повторяется при среднем j₂= (j₁+j₁^I)/2. В результате второй попытки находят j₂^I, сравнивают с предыдущем значением и т.д., пока не достигнуто достаточно близкое совпадение. Обычно требуется 2-3 попытки.