
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Указания по решению отдельных задач
|
|
Каждый вариант контрольной работы включает 4 задачи по наиболее важным разделам курса.
Ответ на 1 вопрос задачи № 1 предполагает изучение темы «Сводка и группировка» и проведение аналитической группировки, с целью выявления зависимости между признаками. В основу аналитической группировки следует положить факторный признак (объем произведенной продукции). Ширина равного интервала определяются по формуле:
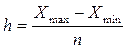 ,
,
где 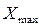 ,
, 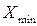 – максимальное и минимальное значение признака,
– максимальное и минимальное значение признака,
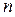 – число групп.
– число групп.
Группировку можно провести, построив ранжированный (упорядоченный) ряд, либо с помощью следующей рабочей таблицы:
| Группы единиц совокупности по объему произведенной продукции, д.е. | Число единиц совокупности | Объем произведенной продукции, д.е. | Валовая прибыль, д.е. |
| 1 группа | |||
| Итого | |||
| 2 группа | |||
| Итого | |||
| n-группа | |||
| Итого | |||
| Всего |
По каждой единице совокупности, отнесенной к той или иной группе, в соответствующей графе записывается значение признака, а в графе «Число единиц» ставится точка. После того, как все заводы будут разнесены по соответствующим группам, подсчитываются групповые итоги и итог всей совокупности.
По результатам рабочей таблицы строится итоговая групповая таблица.
| Группы единиц совокупности по объему произведенной продукции, д.е. | Число единиц совокупности | Объем произведенной продукции, д.е | Валовая прибыль, д.е. | ||
| Всего | На 1единицу | Всего | На 1единицу | ||
| А | 3=2/1 | 5=4/1 | |||
| Итого: |
Сравнивая направление изменения факторного признака и результативного можно выявить зависимость результативного признака от факторного.
Задание №2 задачи №1 составлено по теме «Статистическое изучение связи».
Для изучения взаимосвязи между признаками следует определить параметры линейного уравнения связи (уравнения регрессии).
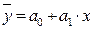 ,
,
где 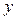 – значения результативного признака;
– значения результативного признака;
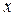 – значения факторного признака;
– значения факторного признака;
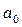 и
и 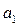 – параметры уравнения регрессии, которые определяют путем решения системы нормальных уравнений:
– параметры уравнения регрессии, которые определяют путем решения системы нормальных уравнений:
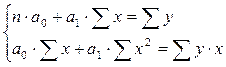
Параметр 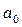 имеет расчетное значение. Знак при коэффициенте
имеет расчетное значение. Знак при коэффициенте  – показывает направление зависимости. Если
– показывает направление зависимости. Если  положительно – связь прямая, отрицательно – связь обратная. Численное значение
положительно – связь прямая, отрицательно – связь обратная. Численное значение  показывает - на сколько единиц увеличивается значение результативного признака при изменении факторного на единицу.
показывает - на сколько единиц увеличивается значение результативного признака при изменении факторного на единицу.
Линейный коэффициент корреляции можно рассчитать по формуле:
 ,
,
где (для несгруппированных данных):
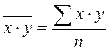 ;
;  ;
; 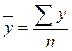 ;
;
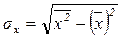 ;
; 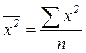 ;
; 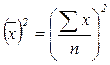 ;
;
 ;
; 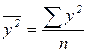 ;
; 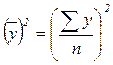 .
.
Линейный коэффициент корреляции характеризует направление и тесноту связи. Если  положителен – связь прямая, отрицателен – обратная. Чем ближе
положителен – связь прямая, отрицателен – обратная. Чем ближе  по модулю к единице, тем теснее связь, чем ближе к нулю – тем слабее.
по модулю к единице, тем теснее связь, чем ближе к нулю – тем слабее.
Расчеты оформляют в виде таблицы
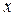
| 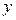
| 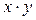
| 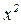
| 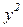
|
Для решения задач 11-20 следует изучить тему «Средние величины». Среднее значение признака в экономической практике определяется по формуле средней арифметической (простой и взвешенной) и средней гармонической (простой и взвешенной). Выбор конкретной формулы расчета среднего уровня зависит от характера исследуемого признака и имеющейся в задаче информации. Основой для выбора формы средней является экономическое содержание осредняемого показателя, понимание того, какое экономическое отношение представляет собой рассматриваемый осредняемый признак, что является исходной базой для расчета среднего значения данного признака.
Например, исходной базой для расчета средней заработной платы будет служить следующее соотношение:
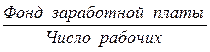 .
.
Если фонд заработной платы обозначить через 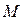 , число рабочих –
, число рабочих – 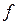 , а среднюю заработную плату –
, а среднюю заработную плату – 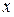 , то
, то
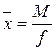 .
.
Допустим, что по условию задачи известна заработная плата 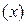 по отдельным подразделениям и численность рабочих
по отдельным подразделениям и численность рабочих  этих подразделений, то фонд заработной платы
этих подразделений, то фонд заработной платы 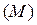 можно найти как произведение
можно найти как произведение 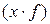 , тогда
, тогда
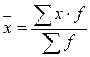 .
.
Если по условию задачи известны по каждому подразделению заработная плата 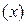 и фонд заработной платы
и фонд заработной платы 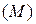 , то численность рабочих
, то численность рабочих 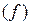 находим путем деления фонда заработной платы на среднюю заработную плату, т.е.
находим путем деления фонда заработной платы на среднюю заработную плату, т.е.
 ,
,
тогда
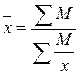 .
.
Средняя величина признака из интервального ряда распределения определяется по формуле средней арифметической взвешенной:
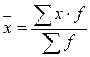 .
.
В качестве значений признака 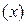 в каждой группе принимается середина интервала, равная полусумме значений нижней и верхней границы интервала. Ширина открытого интервала принимается равной ширине близлежащего интервала.
в каждой группе принимается середина интервала, равная полусумме значений нижней и верхней границы интервала. Ширина открытого интервала принимается равной ширине близлежащего интервала.
Для сокращения трудоемкости расчета средней величины используют «способ моментов», в основе которого лежат следующие свойства средней арифметической:
1) Если все значения признака 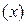 уменьшить (увеличить) на одно и тоже число
уменьшить (увеличить) на одно и тоже число 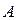 , то и средняя уменьшится (увеличится) на это же число
, то и средняя уменьшится (увеличится) на это же число 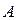 .
.
2) Если все значения признака 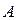 уменьшить (увеличить) в одно и тоже число
уменьшить (увеличить) в одно и тоже число 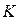 раз, то средняя уменьшится (увеличится) в это же число
раз, то средняя уменьшится (увеличится) в это же число 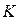 раз.
раз.
Уменьшив все значения признака на величину 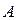 (в качестве
(в качестве 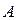 обычно берут значение
обычно берут значение 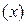 , стоящее в середине вариационного ряда) и, разделив полученные результаты, на
, стоящее в середине вариационного ряда) и, разделив полученные результаты, на 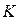 (
(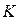 обычно равно ширине интервала), мы найдем условную среднюю:
обычно равно ширине интервала), мы найдем условную среднюю:
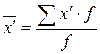 ,
,
где
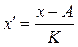 .
.
Фактическая средняя определяется по формуле:
 .
.
МОДА – это значение признака, наиболее часто встречающееся в совокупности.
Мода в дискретном ряду распределения – это значение признака, имеющее наибольшую частоту или частость. Мода в интервальном вариационном ряду определяется по формуле:
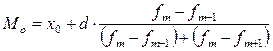 ,
,
где 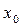 – нижняя граница модального интервала (имеющего наибольшую частоту);
– нижняя граница модального интервала (имеющего наибольшую частоту);
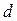 – ширина модального интервала;
– ширина модального интервала;
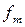 – частота модального интервала;
– частота модального интервала;
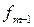 – частота предмодального интервала;
– частота предмодального интервала;
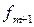 – частота послемодального интервала.
– частота послемодального интервала.
МЕДИАНА – это значение признака у единицы, стоящей в середине ранжированного (упорядоченного) вариационного ряда. Медиана в дискретном ряду – это значение признака, накопленная частота которого содержит единицу, стоящую в середине ранжированного вариационного ряда.
Медиана интервальных вариационных рядов определяется по формуле:
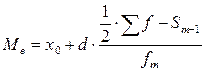 ,
,
где 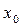 – нижняя граница медианного интервала (накопленная частота которого больше полусуммы всех частот ряда);
– нижняя граница медианного интервала (накопленная частота которого больше полусуммы всех частот ряда);
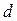 – ширина медианного интервала;
– ширина медианного интервала;
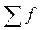 – сумма частот ряда;
– сумма частот ряда;
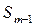 – сумма частот интервалов, предшествующих медианному (накопленная частота);
– сумма частот интервалов, предшествующих медианному (накопленная частота);
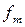 – частота медианного интервала.
– частота медианного интервала.
Решение задач №21-30 предполагает изучение тем «Показатели вариации» и «Выборочное наблюдение».
Показатели вариации.
Среднее линейное отклонение определяют по формуле:
 ,
,
где 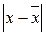 – абсолютное значение отклонения от средней величины в группе;
– абсолютное значение отклонения от средней величины в группе;
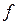 – частота группы.
– частота группы.
ДИСПЕРСИЯ – один из показателей вариации (колеблемости) признака.
Это средний квадрат отклонений от средней величины.
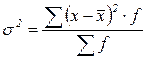 .
.
Используя свойства дисперсии, можно расчет производить по способу моментов.
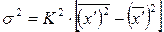 ,
,
где 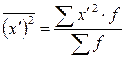 ;
; 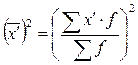 .
.
Для удобства все расчеты оформляют в виде таблицы (таблица 1).
Таблица 1
Расчетная таблица
| Группы единиц изучаемого явления | Число единиц,
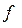
| Середина интервала,
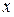
| 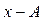
| 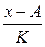 , ,
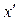
| 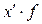
| 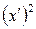
| 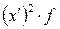
|
| Итого |
Среднее квадратическое отклонение есть корень квадратный из дисперсии.
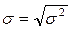
Коэффициент вариации – относительный показатель вариации, выраженный в процентах:
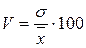 .
.
Дисперсия альтернативного признака определяется по формуле:
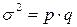 ,
,
где 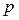 – доля единиц совокупности обладающих данным признаком;
– доля единиц совокупности обладающих данным признаком;
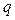 – доля единиц совокупности не обладающих данным признаком.
– доля единиц совокупности не обладающих данным признаком.
Виды дисперсий и правило их сложения
Правило сложения дисперсий: Общая дисперсия равна сумме средней из групповых дисперсий и межгрупповой дисперсии.
 ,
,
где 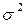 – общая дисперсия,
– общая дисперсия, 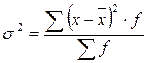 ;
;
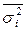 - средняя из групповых дисперсий,
- средняя из групповых дисперсий, 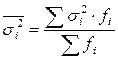 ;
;
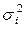 – групповая дисперсия,
– групповая дисперсия, 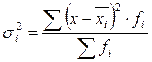 ;
;
где 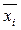 – среднее значение признака
– среднее значение признака 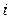 -ой группы;
-ой группы;
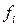 – частота
– частота 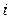 -ой группы;
-ой группы;
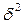 – межгрупповая дисперсия,
– межгрупповая дисперсия, 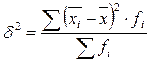 .
.
Выборочное наблюдение
Характеристики выборочной совокупности не совпадают с характеристиками генеральной совокупности.
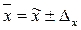 ,
,
где 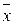 – средняя величина признака в генеральной совокупности;
– средняя величина признака в генеральной совокупности;
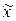 – средняя величина признака в выборочной совокупности;
– средняя величина признака в выборочной совокупности;
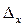 – предельная ошибка выборки.
– предельная ошибка выборки.
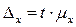 ,
,
где 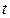 – коэффициент доверия, зависящий от вероятности.
– коэффициент доверия, зависящий от вероятности.
При вероятности равной:
0, 683 коэффициент 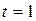 ,
,
0, 954 коэффициент 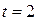 ,
,
0, 997 коэффициент 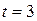 .
.
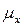 – средняя ошибка выборки для средней.
– средняя ошибка выборки для средней.
 – для собственно-случайной повторной выборки.
– для собственно-случайной повторной выборки.
 – для собственно-случайной бесповторной и механической выборки,
– для собственно-случайной бесповторной и механической выборки,
где 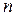 – численность выборочной (отобранной для обследования) совокупности.
– численность выборочной (отобранной для обследования) совокупности.
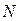 – численность генеральной (всей изучаемой) совокупности.
– численность генеральной (всей изучаемой) совокупности.
Признак, которым каждая единица совокупности или обладает, или не обладает, называется альтернативным.
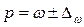 ,
,
где 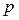 – доля единиц, обладающих данным признаком в генеральной совокупности;
– доля единиц, обладающих данным признаком в генеральной совокупности;
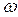 – доля единиц, обладающих данным признаком в выборочной совокупности;
– доля единиц, обладающих данным признаком в выборочной совокупности;
 – предельная ошибка выборки для доли.
– предельная ошибка выборки для доли.
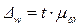
Средняя ошибка выборки при определении доли исчисляется по следующей формуле:
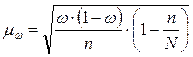 ,
,
где  – дисперсия альтернативного признака.
– дисперсия альтернативного признака.
Относительная ошибка выборки:
- для средней 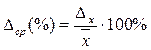 ;
;
- для доли 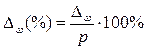 .
.
Задачи 31-40 составлены по теме «Ряды динамики».
Средний уровень интервального ряда динамики абсолютных величин определяется по формуле средней арифметической простой:
 ,
,
где 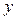 – уровни ряда динамики;
– уровни ряда динамики;
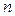 – число уровней.
– число уровней.
Средний уровень моментного ряда динамики рассчитывается:
а) по формуле средней арифметической взвешенной, если есть точные сведения о моменте изменения уровня ряда:
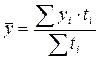 ,
,
где 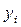 – уровень
– уровень 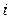 -го периода;
-го периода;
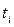 – продолжительность
– продолжительность 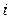 -го периода;
-го периода;
б) если нет точных сведений о моменте изменения ряда, то используют формулу средней арифметической взвешенной из средних величин:
 ,
,
где 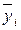 – полусумма уровней на начало и конец
– полусумма уровней на начало и конец 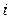 -го периода;
-го периода;
в) если нет точных сведений о моменте изменения ряда, но 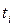 равны между собой, то используется формула средней хронологической:
равны между собой, то используется формула средней хронологической:
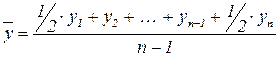 ,
,
где 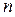 – число уровней ряда динамики.
– число уровней ряда динамики.
Уровень 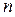 - уровень на конец периода.
- уровень на конец периода.
Абсолютный прирост:
| а) цепной | б) базисный |
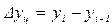
| 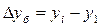
|
в) среднегодовой абсолютный прирост:
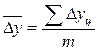 или
или 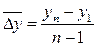 ,
,
где 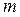 - число
- число 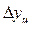 .
.
Темп роста:
а) цепной 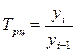 или
или 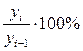 ;
;
б) базисный 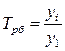 или
или 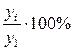 .
.
Произведение цепных темпов роста равно соответствующему базисному темпу роста.
в) среднегодовой темп роста:
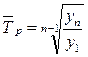 или
или 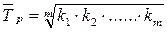 ,
,
где 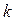 – цепные темпы роста, выраженные в коэффициентах;
– цепные темпы роста, выраженные в коэффициентах;
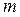 – число цепных темпов роста.
– число цепных темпов роста.
Темп прироста:
а) цепной 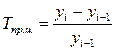 или
или  ;
;
б) базисный 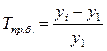 или
или 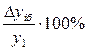 .
.
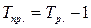 .
.
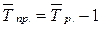 или
или 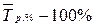 .
.
Абсолютное значение одного процента прироста равно 0, 01 доле предыдущего уровня:
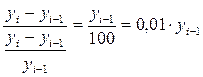 .
.
Результаты расчета представить в таблице:
Показатели анализа ряда динамики
| Год | Уровни | Абсолютный прирост | Темп роста | Темп прироста | Абсол. знач. 1% прироста | |||
| Цепной | Базисный | Цепной | Базисный | Цепной | Базисный | |||
Аналитическое выравнивание по прямой предполагает нахождение параметров уравнения:
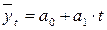 ,
,
где 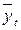 – выравненные (теоретические) уровни ряда динамики;
– выравненные (теоретические) уровни ряда динамики;
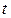 – показатель времени;
– показатель времени;
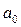 и
и 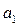 – параметры уравнения, которые определяются решением следующей системы нормальных уравнений.
– параметры уравнения, которые определяются решением следующей системы нормальных уравнений.
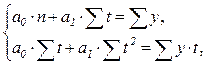
где 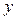 – фактические уровни ряда динамики;
– фактические уровни ряда динамики;
 – число уровней ряда;
– число уровней ряда;
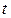 – условное обозначение времени.
– условное обозначение времени.
Если начало условного отсчета времени поместить в середину изучаемого периода, то 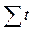 будет равна 0.
будет равна 0.
При нечетном числе периодов (моментов) времени:
| -2 | -1 | +1 | +2 |
При четном числе периодов (моментов) времени:
| -5 | -3 | -1 | +1 | +3 | +5 |
Это значительно упрощает решение системы уравнений, т.к. при 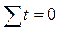 она примет следующий вид:
она примет следующий вид:
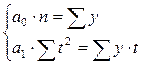 ,
,
отсюда 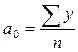 ,
, 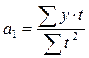 .
.
Расчеты целесообразно выполнить в следующей таблице:
| Годы | Эмпирический ряд,
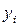
| Условные обозначения дат,
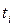
| 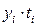
| 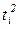
| Выравненный ряд динамики,
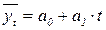
|
Правильность расчета выравненных уровней доказывает равенство:
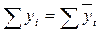 .
.
Используя определенное таким образом уравнение общей тенденции (тренда) развития, можно дать прогноз на будущее (экстраполяция) придав соответствующее значение 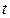 для года, на который дается прогноз.
для года, на который дается прогноз.
Решение задачи 41-50 предполагает изучение темы «Индексный анализ».
В теории и практике статистики разработана символика и применяются следующие условные обозначения:
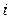 – индивидуальные индексы;
– индивидуальные индексы;
 – общие индексы;
– общие индексы;
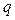 – объем продукции, товаров и т.д.;
– объем продукции, товаров и т.д.;
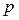 – цена;
– цена;
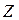 или
или  – себестоимость;
– себестоимость;
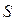 или
или 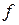 – заработная плата;
– заработная плата;
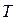 – общие затраты труда;
– общие затраты труда;
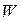 – выработка;
– выработка;
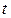 – трудоемкость.
– трудоемкость.
Значениям базисного периода придается знак «0», отчетного – «1».
Индивидуальные индексы исчисляются по формулам:
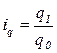 ;
; 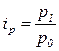 ;
; 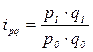 .
.
При построении агрегатных формул общих индексов следует учитывать правило: если индексируемая величина – качественный показатель, то веса берут на уровне отчетного периода; если индексируемая величина – количественный показатель, то веса берут на уровне базисного периода.
В индексе стоимости продукции в качестве индексируемой величины выступает стоимость продукции, равная произведению цены на количество продукции 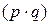 .
.
Поэтому:
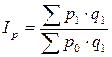 ,
, 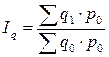 ,
, 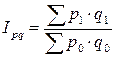 .
.
Индексы, как относительные величины характеризуют изменение явления в коэффициентах или процентах.
Абсолютное выражение изменения стоимости продукции можно определить, как разницу между числителем и знаменателем индекса стоимости продукции:
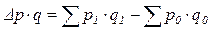 .
.
Данная система индексов позволяет разложить изменение общей величины по факторам. Поскольку стоимость продукции есть результат действия двух факторов (цены и объема производства), то изменение каждого из них влечет за собой изменение и стоимости продукции. Изменение стоимости за счет изменения цены определим как разницу между числителем и знаменателем индекса цен:
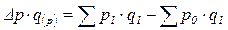 ,
,
а за счет изменения объема продукции – как разницу между числителем и знаменателем индекса физического объема продукции:
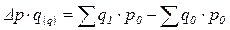 .
.
При этом 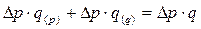 .
.
Между индексами существует та же взаимосвязь, что и между явлениями. Поскольку стоимость продукции есть произведение цен и объема продукции, то и индекс стоимости продукции равен произведению индекса цен и индекса физического объема продукции.
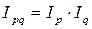 .
.
Так же взаимосвязаны и индексы затрат на производство, себестоимости и физического объема продукции:
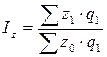 ,
, 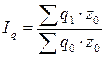 ,
, 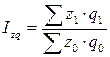 ,
,
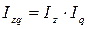 .
.
Расчет индексов по агрегатным формулам возможен, если есть полные данные как об индексируемой величине, так и о весах на отчетном и базисном уровне. Если таких данных нет, то приходится исчислять индексы как среднюю взвешенную величину из индивидуальных индексов.
Используются формулы среднеарифметического и среднегармонического индексов:
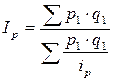 ,
, 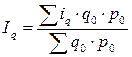 .
.
При выборе формы средней следует иметь ввиду, что агрегатный индекс – основная форма всякого индекса и средний из индивидуальных будет тогда правильным, когда он тождествен агрегатному.
При индексном анализе динамики средних уровней качественного показателя исчисляют индексы переменного и постоянного состава.
Индекс переменного состава характеризует изменение средней величины качественного показателя по всей совокупности:
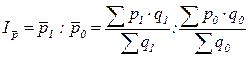 .
.
Индекс постоянного состава характеризует изменение величины качественного показателя в среднем по отдельным объектам совокупности:
 .
.
Как видно из формулы, на величину индекса переменного состава оказывает влияние изменение самих цен и изменение состава (структуры) продукции. Для выявления влияния на изменение средней величины изменения структуры продукции исчисляют индекс влияния структурных сдвигов.
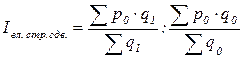 .
.
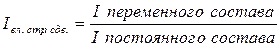 .
.
Индивидуальные индексы производительности труда могут быть рассчитаны по формулам:
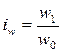 или
или 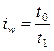 ,
,
где 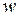 – выработка продукции в единицу времени;
– выработка продукции в единицу времени;
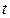 – затраты труда на единицу продукции.
– затраты труда на единицу продукции.
Общие индексы производительности труда постоянного состава рассчитывают по формулам:
а) 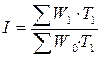 , где
, где 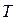 – затраты труда на весь объем продукции.
– затраты труда на весь объем продукции.
б) 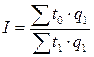 , где
, где 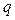 – объем продукции.
– объем продукции.
Индексы производительности труда переменного состава:
а) 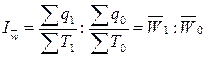 .
.
Это натуральный индекс, он может быть использован при одноименной продукции.
б) Если продукция разноименная, используют стоимостной индекс производительности труда:
 ,
,
где 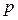 – цена единицы продукции.
– цена единицы продукции.
Общий индекс производительности труда можно рассчитать как средний арифметический из индивидуальных индексов (индекс С.Г. Струмилина):
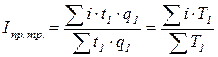 .
.
|
|