💸 Как сделать бизнес проще, а карман толще?

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое раписание, но и напоминать клиентам о визитах тоже. Проблема в том, что средняя цена по рынку за такой сервис — 800 руб/мес или почти 15 000 руб за год. И это минимальный функционал. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
⚡️ Для новых пользователей первый месяц бесплатно. А далее 290 руб/мес, это в 3 раза дешевле аналогов. За эту цену доступен весь функционал: напоминание о визитах, чаевые, предоплаты, общение с клиентами, переносы записей и так далее.
✅ Уйма гибких настроек, которые помогут вам зарабатывать больше и забыть про чувство «что-то мне нужно было сделать».
Сомневаетесь? нажмите на текст, запустите чат-бота и убедитесь во всем сами!

Элементы корреляционного анализа

Вариант №18

Дано: Результаты исследований зависимости между случайными величинами X и Y представлены в виде таблицы 8:

Таблица №8

Произвести корреляционный анализ зависимости Y от X, для чего:
Построить корреляционное поле;

1. Найти выборочный коэффициент корреляции ;

2. Получить доверительный интервал r_xy для с надежностью γ;

3. Найти выборочное уравнение прямой регрессии Y на X;

4. В выбранной системе координат построить точки (x_i, y_i) и выборочное уравнение регрессии Y на X.

§1. Корреляционная таблица и корреляционное поле

Представим данные корреляционной таблицы в виде корреляционного поля. Для этого в выбранной системе координат изобразим точки (x_i, y_j) и рядом с каждой точкой укажем, если это позволит масштаб, соответствующую частоту n_xy. По расположению точек можно сделать предположение о наличии (или отсутствии) линейной корреляционной зависимости между обследуемыми признаками X и Y.

Для данных таблицы 8 корреляционное поле имеет вид:

Расположение точек говорит о наличии положительной корреляции между признаками X и Y.

§2. Нахождение выборочного коэффициента корреляции

Вычисления можно значительно упростить, если перейти от истинных вариант x_i, y_j к условным u_i, v_j соответственно, а именно:

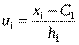
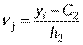
C1 = 45 h1 = 5 u1 = -3 u2 = -2 u3 = -1 u4 = 0 u5 = 1 u6 = 2	C2 = 65 h2 = 10 v1 = -1 v2 = 0 v3 = 1 v4 = 2

Формула для вычисления эмпирического коэффициента корреляции в условных вариантах имеет вид:

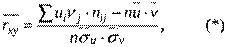
Для нахождения 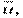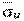составим расчетную таблицу 9.

Таблица №9

Контроль

_,

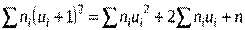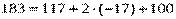
то есть вычисления верны

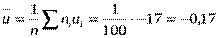
Так как 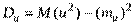, то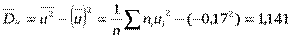

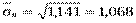
Аналогичные вычисления проводим для v в таблице 10.

Таблица №10

ui vj	-3	-2	-1	0	1	2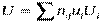
-3			-12			-4													-16	48
	4			2
-12			-6
-2						-10			-3										-13	26
				5			3
			-10			-6
-1						-			-5			0			5				0	0
							5			45			5
						-5			-45			-5
0									-7			0			2			0	-5	0
							7			8			2
						0			0			0
1												0			3				17	17
										4			3
									4			3
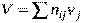
	-12	-16	-11	-41	-2	7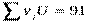
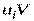
	36	32	11	0	-2	14		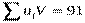контроль

Контроль вычислений производим по формуле:

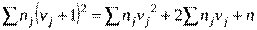
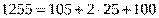
вычисления верны.

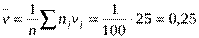
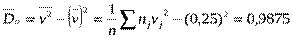
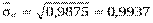
Для вычисления 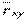требуется еще найти 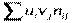. Для ее нахождения составим корреляционную таблицу 11 в условных вариантах.

Подставив найденные значения в формулу (*), получим

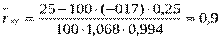
Таблица №11

§3. Нахождение доверительного интервала
для генерального коэффициента корреляции

Задана надежность γ = 0, 99. Доверительный интервал для генерального коэффициента корреляции r_xy имеет вид:

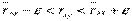
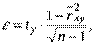
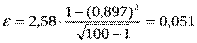
Следовательно с вероятностью 0, 99 доверительный интервал имеет вид:

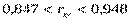
§4. Нахождение выборочного уравнения прямой регрессии Y на X и построение ее графика

Общий вид уравнения прямой линии регрессии Y на X имеет вид:

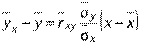
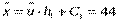
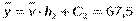
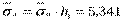
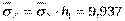
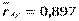
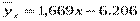
Полученное уравнение регрессии показывает, как в среднем изменяется значение признака Y в зависимости от изменения признака Х.
В выбранной системе координат строим прямую 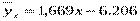и точки (x_i, y_i) корреляционного поля.

Таблица для построения графика

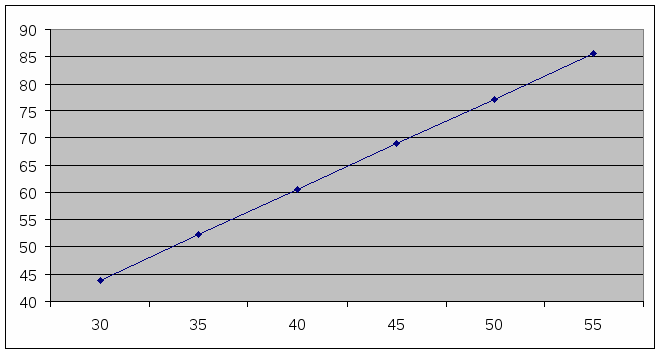
ВЫВОД: Построив корреляционное поле мы убеждаемся, что расположение точек говорит о наличии положительной корреляции между Х и Y. По расположению точек можно судить о линейной зависимости между Х и Y.

Заключение

В проделанной курсовой работе была предоставлена возможность проверить гипотезу Пирсона, опираясь на полученные результаты, я могу утверждать, что эмпирические и теоретические частоты различаются незначительно. Так же был проведен корреляционный анализ, была выявлена сильная линейная зависимость между величинами X и Y

Список использованной литературы

1. Гмурман В.Е. «Теория вероятностей математической статистики» – М.: Высшая школа, 1999 г.

2. «Пособие и методические указания к выполнению курсовой работы» – Калининград: 1998 г.