
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Ціна за 1 грам золота, грн. на станом на 10.06.2015
|
|
| Проба | Ціна | ||
| Звичайний кредит | Срібна картка | Золота картка | |
За даними Мережі ломбардів «Комод»[]
Для побудови економіко-математичної моделі введемо наступні позначення:
· і - номер групи дорогоцінних металів за пробами (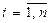 );
);
· 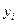 ,
, 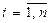 - закупівельна ціна 1 грама дорогоцінного металу, грн.;
- закупівельна ціна 1 грама дорогоцінного металу, грн.;
· 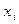 ,
, 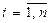 - ціна продажу 1 г дорогоцінного металу, грн.
- ціна продажу 1 г дорогоцінного металу, грн.
На обмеженій області класичні нелінійні криві попиту і пропозиції, мають властивість сепарабельності, тобто їх можна представити сумою відрізків прямих ліній: i.
Крива пропозиції клієнтом ломбарду і-го виду дорогоцінного металу за планом:
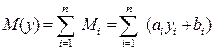 (3.1)
(3.1)
Крива попиту на незатребувані дорогоцінні метали i -ого виду покупцями, в магазині при ломбарді за планом
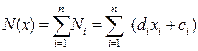 (3.2)
(3.2)
де 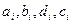 ,
, 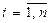 - коефіцієнти, що характеризують особливості попиту і пропозиції дорогоцінних металів за групами в ломбарді.
- коефіцієнти, що характеризують особливості попиту і пропозиції дорогоцінних металів за групами в ломбарді.
При цьому існує залежність між 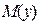 та
та 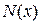 виявлена експертним методом по кожній групі дорогоцінних металів:
виявлена експертним методом по кожній групі дорогоцінних металів:
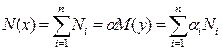 ,
, 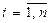 (3.3)
(3.3)
де 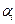 – частка не викуплених виробів, по кожній групі дорогоцінних металів від загального обсягу застави.
– частка не викуплених виробів, по кожній групі дорогоцінних металів від загального обсягу застави.
З врахуванням прийнятих позначень економіко-математична модель оптимізації закупівельної ціни та ціни продажу на дорогоцінні метали у ломбарді, що максимізує прибуток підприємства, має вигляд:
1) Ціль: максимізація прибутку від даного виду діяльності ломбарду, грн:
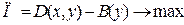 (3.4)
(3.4)
де 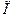 - прибуток від покупки та продажу дорогоцінних металів у ломбарді, грн;
- прибуток від покупки та продажу дорогоцінних металів у ломбарді, грн;
 - дохід від покупки та продажу дорогоцінних металів у ломбарді, грн;
- дохід від покупки та продажу дорогоцінних металів у ломбарді, грн;
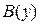 - витрати на придбання, кредитування та утримання і-го виду дорогоцінного металу, грн.
- витрати на придбання, кредитування та утримання і-го виду дорогоцінного металу, грн.
2) Обмеження моделі:
а) умова рівності обсягу закупівель і продаж з урахуванням коефіцієнту 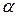
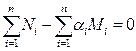 (3.5)
(3.5)
б) невід’ємність функцій попиту та пропозиції
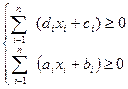 ,
, 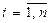 (3.6)
(3.6)
в) невід’ємність змінних моделі:
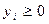 ,
, 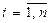 ,
, 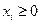 ,
, 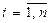 (3.7)
(3.7)
Для визначення оптимального прибутку розрахуємо окремі показники та коефіцієнти для моделі (3.4-3.7).
Дохід від продажу дорогоцінних металів за планом ломбарду, яка складається з декількох складових, дорівнює.
 (3.8)
(3.8)
Враховуючи, що витрати ломбарду по організації торгівлі та придбанні дорогоцінних металів дорівнюють:
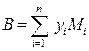 (3.9)
(3.9)
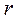 - ставка ломбарду по наданих кредитах, частин;
- ставка ломбарду по наданих кредитах, частин;
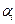 - частка не викуплених виробів, по кожній групі дорогоцінних металів від загального обсягу застави, %, запланована на наступний період.
- частка не викуплених виробів, по кожній групі дорогоцінних металів від загального обсягу застави, %, запланована на наступний період.
Формула для розрахунку доходу ломбарду від продажу та купівлі дорогоцінних металів набуває вигляду:
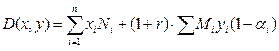 (3.10)
(3.10)
Для показників попиту 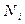 та
та  пропозиції ми пропонуємо наступну методику їх обґрунтування:
пропозиції ми пропонуємо наступну методику їх обґрунтування:
Введемо додаткові позначення з урахуванням різних варіантів (індекси 1 і 2) за планом:
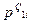 ,
, 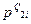 – можливі закупівельні ціни 1 г дорогоцінного металу і -ої проби у клієнта ломбарду, грн;
– можливі закупівельні ціни 1 г дорогоцінного металу і -ої проби у клієнта ломбарду, грн;
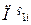 ,
, 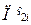 – прогнозований обсяг купівлі 1 г дорогоцінного металу і -ої проби у клієнта ломбарду за ціною
– прогнозований обсяг купівлі 1 г дорогоцінного металу і -ої проби у клієнта ломбарду за ціною 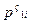 та
та 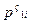 відповідно;
відповідно;
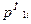 ,
,  і – можливі ціни продажу 1 г дорогоцінного металу і -ої проби за планом, грн;
і – можливі ціни продажу 1 г дорогоцінного металу і -ої проби за планом, грн;
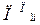 ,
, 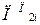 – прогнозований обсяг продажу магазином при ломбарді 1 г дорогоцінного металу і -ої проби за планом за цінами
– прогнозований обсяг продажу магазином при ломбарді 1 г дорогоцінного металу і -ої проби за планом за цінами 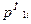 ,
,  відповідно.
відповідно.
Апроксимація кривих пропозиції 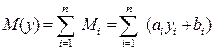 та попиту
та попиту 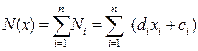 , дає наступні результати:
, дає наступні результати:
Для пропозиції
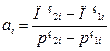 (3.11)
(3.11)
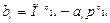 (3.12)
(3.12)
Для визначення попиту:
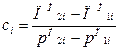 (3.13)
(3.13)
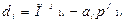 (3.14)
(3.14)
Підставляючи отримані коефіцієнти у модель (3.4-3.6) ми отримаємо усі дані для розв’язку економіко-математичної моделі оптимізації закупівельної ціни та ціни продажу на дорогоцінні метали у ломбарді, що максимізує прибуток ломбарду.
Пропонована модель є задачею нелінійного математичного програмування. Для її вирішення сучасні комп'ютери мають стандартний набір програм, наприклад «Пошук рішення» в MS Excel. В процедурі пошуку рішення Microsoft Excel використовується алгоритм нелінійної оптимізації Generalized Reduced Gradient (GRG2), розроблений Леоном Ласдоном (Leon Lasdon, University of Texas at Austin)[] і Аланом Уорен (Allan Waren, Cleveland State University)[]. Алгоритми симплексного методу і методу " branch-and-bound" для вирішення лінійних і целочисельних задач з обмеженнями розробленими Джоном Уотсоном (John Wat-son)[] і Деном Філстра (Dan Fylstra)[] з Frontline Systems, Inc.
Розглянемо числовий приклад рішення цієї задачі. Маємо вхідні дані по планах та прогнозах цін та обсягів покупки та продажу дорогоцінних металів при ставки відсотку 45% табл. 3.6.
Таблиця 3.6
|
|