
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Общая схема градиентных методов. Понятие функции релаксации
|
|
Пусть решается задача
 (5.1)
(5.1)
Рассмотрим класс матричных градиентных методов вида
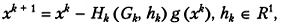 (5.2)
(5.2)
где 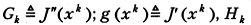 — матричная функция от
— матричная функция от 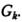 Предполагается, что в некоторой
Предполагается, что в некоторой 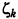 -окрестности
-окрестности 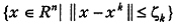 точки
точки  функционал J (x) достаточно точно аппроксимируется параболоидом
функционал J (x) достаточно точно аппроксимируется параболоидом
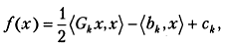 (5.3)
(5.3)
где 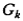 — симметричная, не обязательно положительно определенная матрица. Без существенного ограничения общности можно считать, что
— симметричная, не обязательно положительно определенная матрица. Без существенного ограничения общности можно считать, что 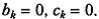 Действительно, полагая
Действительно, полагая 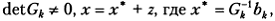 получим представление
получим представление
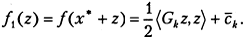 (5.4)
(5.4)
При этом константа  может не учитываться как не влияющая на процесс оптимизации.
может не учитываться как не влияющая на процесс оптимизации.
Формула (5.2) обладает свойством инвариантности относительно смещения начала координат: будучи записанной для f (x), она преобразуется в аналогичное соотношение для f 1(z). А именно, имеем для f (x)
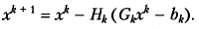 (5.5)
(5.5)
Полагая 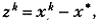 получим из (5.5):
получим из (5.5): 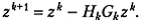 А это есть запись метода (5.2) для функционала f 1.
А это есть запись метода (5.2) для функционала f 1.
 Ставится задача построения таких матричных функций
Ставится задача построения таких матричных функций 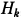 , чтобы выполнялись условия релаксационности процесса
, чтобы выполнялись условия релаксационности процесса 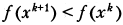 и чтобы при этом величина нормы
и чтобы при этом величина нормы 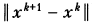 ограничивалась сверху только параметром
ограничивалась сверху только параметром 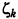 , характеризующим область справедливости локальной квадратичной модели (5.3). При высокой степени овражности
, характеризующим область справедливости локальной квадратичной модели (5.3). При высокой степени овражности 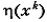 для большинства классических схем поиска имеем
для большинства классических схем поиска имеем 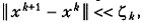 что в результате приводит к медленной сходимости.
что в результате приводит к медленной сходимости.
Определение 5.1. Скалярная функция 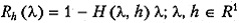 называется функцией релаксации метода (5.2), а ее значения R h (λ i) на спектре матрицы
называется функцией релаксации метода (5.2), а ее значения R h (λ i) на спектре матрицы 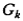 — множителями релаксации для точки
— множителями релаксации для точки 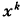 .
.
В ряде случаев для сокращения записи индекс «h» в выражении для функции релаксации будет опускаться.
Здесь Н (λ, h) означает скалярную зависимость, отвечающую матричной функции H (G, h) в представлении (5.2).
Если G — симметричная матрица и
G = T diag (λ 1, λ 2,... λ n) T T,
где Т — ортогональная матрица, столбцы которой есть собственные векторы матрицы G, то любая матричная функция F (G) представима в виде
F (G) = T diag(F (λ 1), F (λ 2),... F (λ n)) T T,
Матричная функция F (G) имеет смысл, если скалярная функция F (λ) определена в точках λ 1, λ 2,... λ n.
Теорема 5.1. Для выполнения условия
 (5.6)
(5.6)
при  необходимо и достаточно, чтобы
необходимо и достаточно, чтобы
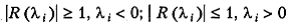 (5.7)
(5.7)
для всех собственных чисел λ i, i ∈ [1: n ], матрицы 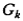 .
.
Замечание 1. Для строгого выполнения неравенства (5.6) необходимо и достаточно кроме (5.7) потребовать, чтобы существовал такой i = i 0, для которого 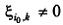 и соответствующее неравенство (5.7) было строгим.
и соответствующее неравенство (5.7) было строгим.
Замечание 2. Выражения (5.8) позволяют оценить скорость убывания функционала f в зависимости от «запаса», с которым выполняются неравенства (5.7). Действительно, обозначим через 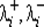 положительные и отрицательные собственные числа матрицы
положительные и отрицательные собственные числа матрицы 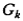 . Этими же индексами снабдим соответствующие собственные векторы. Суммирование по соответствующим i будем обозначать Σ +, Σ –. Тогда
. Этими же индексами снабдим соответствующие собственные векторы. Суммирование по соответствующим i будем обозначать Σ +, Σ –. Тогда
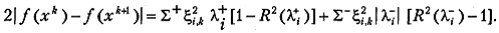
Из полученного выражения следует, что наибольшее подавление будут испытывать слагаемые, для которых значение множителя релаксации наиболее существенно отличается от единицы (при выполнении условий (5.7)).
Далее будут рассматриваться в основном зависимости Rh (λ), обладающие свойством
Rh (λ) → 1, h → 0, (5.9)
В этом случае из равенства
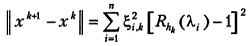
следует, что для 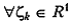 всегда можно выбрать такой
всегда можно выбрать такой  , что
, что 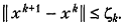 Таким образом, с помощью параметра
Таким образом, с помощью параметра  можно регулировать норму вектора продвижения в пространстве управляемых параметров с целью предотвращения выхода из области справедливости локальной квадратичной модели (5.3).
можно регулировать норму вектора продвижения в пространстве управляемых параметров с целью предотвращения выхода из области справедливости локальной квадратичной модели (5.3).
Иногда для ограничения нормы (5.10) параметр h может вводиться в схему оптимизации как множитель в правой части (5.2):
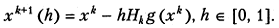 (5.11)
(5.11)
При этом 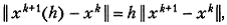 а второе равенство (5.8) трансформируется к виду
а второе равенство (5.8) трансформируется к виду
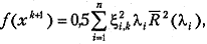
где 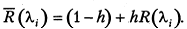 Таким образом, новые множители релаксации
Таким образом, новые множители релаксации 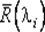 принимают промежуточные значения между 1 и R (λ i), что и требуется для обеспечения свойства релаксационности, определяемого требованиями (5.9).
принимают промежуточные значения между 1 и R (λ i), что и требуется для обеспечения свойства релаксационности, определяемого требованиями (5.9).
Введенное понятие функции релаксации позволяет с единых позиций оценить локальные свойства различных градиентных схем поиска. Удобство такого подхода заключается также в возможности использования наглядных геометрических представлений. Подобно областям устойчивости методов численного интегрирования обыкновенных дифференциальных уравнений, построенных на основе «тестового» (линейного, скалярного) уравнения, мы можем для любого метода (5.2) построить функцию релаксации, характеризующую область его релаксационности в множестве собственных чисел матрицы Гессе аппроксимирующего параболоида. При этом роль тестового функционала играет квадратичная зависимость (5.3). Требуемый характер функции релаксации представлен на рис. 5.1; заштрихована «запрещенная» область, где условия релаксационности (5.7) не выполняются.
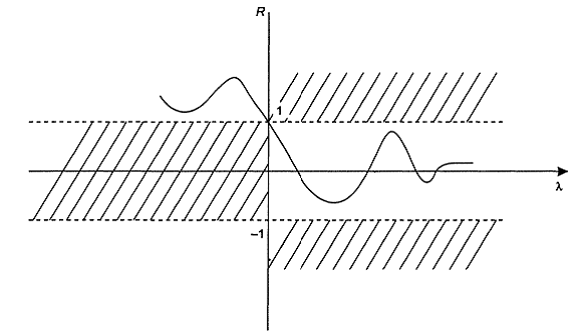
Рис. 5.1. Общий вид функции релаксации
Важное свойство функций релаксации заключается в возможности использования соответствующих представлений для синтеза новых процедур (5.2), обладающих некоторыми желательными свойствами при решении конкретных классов задач параметрической оптимизации.
Простой градиентный спуск (ПГС)
Формула метода ПГС имеет вид
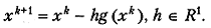 (5.12)
(5.12)
Соответствующая функция релаксации линейна (рис. 5.2):
R (λ) = 1 – λ h. (5.13)
Пусть собственные значения матрицы 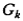 расположены в замкнутом интервале [ т, М ], причем М > > m > 0, так что
расположены в замкнутом интервале [ т, М ], причем М > > m > 0, так что 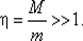 В этом случае условие (5.9), очевидно, выполняется, а неравенства (5.7) сводятся к требованию | R (λ i)| ≤ 1, i ∈ [1: n ], или
В этом случае условие (5.9), очевидно, выполняется, а неравенства (5.7) сводятся к требованию | R (λ i)| ≤ 1, i ∈ [1: n ], или
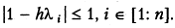 (5.14)
(5.14)
Эти оценки иллюстрируются рис. 5.2. Точка пересечения прямой R (λ) с осью абсцисс есть точка 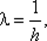 и чтобы при λ ∈ [ т, М ] зависимость R (λ) находилась в разрешенной области, необходимо выполнение неравенства
и чтобы при λ ∈ [ т, М ] зависимость R (λ) находилась в разрешенной области, необходимо выполнение неравенства 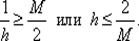 При этом ординаты функции релаксации характеризуют величину соответствующих множителей релаксации, которые в окрестности λ = т будут тем ближе к единице, чем больше величина
При этом ординаты функции релаксации характеризуют величину соответствующих множителей релаксации, которые в окрестности λ = т будут тем ближе к единице, чем больше величина 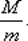 Будем считать, что для собственных чисел матрицы
Будем считать, что для собственных чисел матрицы 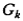 выполняются неравенства
выполняются неравенства
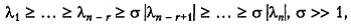
характерные для овражной ситуации. Тогда для точки  где Q — дно оврага, имеем, согласно (5.10),
где Q — дно оврага, имеем, согласно (5.10),

что может быть существенно меньше 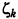 .
.
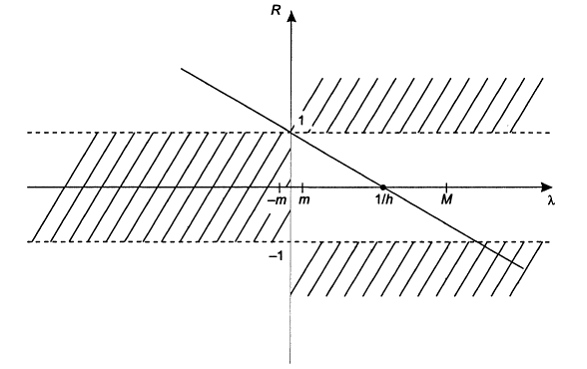
Рис. 5.2. Функция релаксации метода простого градиентного спуска
В результате соответствующие малым собственным значениям из окрестности λ = 0 слагаемые в (5.8) практически не будут убывать, а продвижение будет сильно замедленным. Это и определяет низкую эффективность метода (5.12).
В области λ < 0 функция (5.13) удовлетворяет условиям релаксации при любом значении параметра h. Практически параметр h в методе ПГС выбирается из условия монотонного убывания функционала на каждом шаге итерационного процесса. При отсутствии убывания величина h уменьшается до восстановления релаксационности процесса. Существуют различные стратегии выбора h, однако при больших η все эти методы, включая и метод наискорейшего спуска
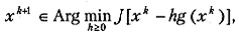
ведут себя приблизительно одинаково плохо даже при минимизации сильно выпуклых функционалов. Так же, как и в методе покоординатного спуска, здесь возможна ситуация заклинивания, представленная на рис. 5.3.
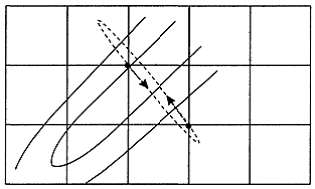
Рис. 5.3. Остановка метода ПГС в овражной ситуации
Метод ПГС представляет определенный интерес как средство оценки локальной степени овражности в окрестности точки замедления алгоритма. Выведем соответствующие соотношения.
Пусть замедление метода ПГС при минимизации некоторого функционала J (x) произошло в окрестности некоторой точки x 0. Тогда можно предположить, что достаточно длинный отрезок последовательности 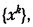 построенной из точки x 0, будет оставаться в области || х – x 0|| ≤ ζ 0, и для J (x) справедлива квадратичная аппроксимация
построенной из точки x 0, будет оставаться в области || х – x 0|| ≤ ζ 0, и для J (x) справедлива квадратичная аппроксимация
 (5.15)
(5.15)
Метод (5.12) для (5.15) примет вид
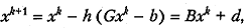 (5.16)
(5.16)
где 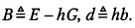
Записывая (5.16) для двух последовательных номеров 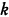 и вычитая полученные равенства, приходим к соотношению
и вычитая полученные равенства, приходим к соотношению
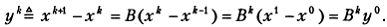 (5.17)
(5.17)
Согласно хорошо известному из курса численного анализа степенному методу определения максимального собственного числа симметричной матрицы, в результате проведения процесса (5.17) может быть получена оценка максимального собственного числа матрицы B:
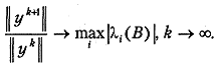 (5.18)
(5.18)
Полагая, что шаг h в итерационном процессе (5.16) выбирается из условия релаксационности (5.7), можно заключить, что 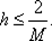 Построив график функции М релаксации 1 – h λ как функции от λ при фиксированном h, легко установить, что при
Построив график функции М релаксации 1 – h λ как функции от λ при фиксированном h, легко установить, что при 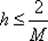 будем иметь
будем иметь
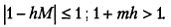
Таким образом,
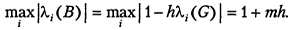
Следовательно, для достаточно больших 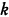 .
.
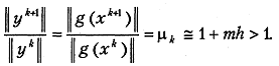 (5.19)
(5.19)
В результате приходим к требуемой оценке степени овражности функционала J (x) в окрестности точки x 0:
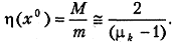
Практически поступают следующим образом. Проводят релаксационный процесс (5.16) до тех пор, пока он не замедлится и отношение 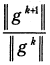 не стабилизируется около некоторого значения
не стабилизируется около некоторого значения 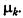 Далее используют полученную оценку степени овражности для выбора последующей стратегии оптимизации.
Далее используют полученную оценку степени овражности для выбора последующей стратегии оптимизации.
Рассуждая аналогично, для случая λ ∈ [ т, М ] из того же графика получим вместо (5.19) равенство 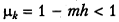 и соответствующую оценку
и соответствующую оценку 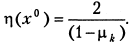 Легко геометрически видеть, что в этом случае для более устойчивого выделения в качестве максимального по модулю собственного числа матрицы В значения 1 – mh достаточно проводить процесс (5.16) с уменьшенным шагом h. Например, на практике удобно в любом случае осуществлять «лишнее» деление шага h на два после получения устойчивой релаксации.
Легко геометрически видеть, что в этом случае для более устойчивого выделения в качестве максимального по модулю собственного числа матрицы В значения 1 – mh достаточно проводить процесс (5.16) с уменьшенным шагом h. Например, на практике удобно в любом случае осуществлять «лишнее» деление шага h на два после получения устойчивой релаксации.
Общая оценка может быть записана в виде
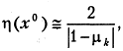
причем, сравнивая 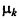 с единицей, можно установить характер выпуклости J (х) в окрестности точки x 0, что дает дополнительную полезную информацию.
с единицей, можно установить характер выпуклости J (х) в окрестности точки x 0, что дает дополнительную полезную информацию.
|
|